- Home
- Assessments
- Bioregional Assessment Program
- Gloucester subregion
- 2.6.2 Groundwater numerical modelling for the Gloucester subregion
- 2.6.2.8 Uncertainty analysis
- 2.6.2.8.2 Qualitative uncertainty analysis
The major assumptions and model choices underpinning the Gloucester subregion groundwater models are listed in Table 11. The goal of the table is to provide a non-technical audience with a systematic overview of the model assumptions, their justification and effect on predictions, as judged by the modelling team. This table is aimed to assist in an open and transparent review of the modelling.
In the table, each assumption is scored on four attributes using three levels; high, medium and low. Beneath the table, each of the assumptions are discussed in detail, including the rationale for the scoring. The ‘data’ attribute is the degree to which the question ‘if more or different data were available, would this assumption/choice still have been made?’ would be answered positively. A ‘low’ score means that the assumption is not influenced by data availability while a ‘high’ score would indicate that this choice would be revisited if more data were available. Closely related is the ‘resources’ attribute. This column captures the extent to which resources available for the analysis and processing of the available data and the modelling, such as computing resources, personnel and time, influenced this assumption or model choice. This attribute does explicitly not consider spending additional resources on data acquisition, as this is covered in the data attribute. Again, a ‘low’ score indicates the same assumption would have been made with unlimited resources, while a ‘high’ value indicates the assumption is driven by resource constraints. The ‘technical’ attribute deals with the technical and computational issues. A score of ‘high’ is assigned to assumptions and model choices that are dominantly driven by computational or technical limitations of the model code. These include issues related to spatial and temporal resolution of the models.
The final, and most important column, ‘effect on predictions’, addresses the ‘so what?’ question, the effect of the assumption or model choice on the predictions. This is a qualitative assessment by the modelling team of the extent to which a model choice will affect the model predictions, with ‘low’ indicating a minimal effect and ‘high’ a large effect. Especially for the assumptions with a large potential impact on the predictions, it will be discussed that the precautionary principle is applied; that is, the hydrological change is overestimated rather than underestimated.
While this table is primarily intended to elaborate on the effects of model assumptions and choices, it can provide guidance for further research. A large number of assumptions in the Gloucester subregion are mainly driven by the limited data and knowledge base. The effect on predictions column indicates which ones are considered to have the largest effect on predictions. The conclusions and opportunities section (Section 2.6.2.9) uses this table to identify the main knowledge and data gaps.
Table 11 Qualitative uncertainty analysis as used for the Gloucester subregion
CSG = coal seam gas
Hybrid analytic element-MODFLOW methodology
Section 2.6.2.1 outlines the overarching hybrid methodology in which analytic element modelling is used at the regional scale in combination with a high resolution MODFLOW model to represent the alluvium. Although not widespread, several studies are available in which analytic element models are combined with MODFLOW models (Hunt, 2006; Abrams et al., 2015).
The choice for the hybrid methodology in this case is mostly driven between the spatial and temporal scale mismatch between the regional groundwater flow in the surface weathered and fractured rock layer and deeper sedimentary basin and the local groundwater flow in the alluvial deposits. To simulate groundwater flow dynamics in both systems in a single model would necessitate a high spatial and temporal resolution. The hybrid approach allows to simulate the regional groundwater flow with a low spatial and temporal resolution, while the alluvial models are simulated with a high spatial and temporal resolution.
Although a geological model was developed to gain additional insight in the stratigraphy and structural features of the region, its resolution and extent are not sufficient to justify such a high-resolution regional-scale finite-difference groundwater model (see companion product 2.1-2.2 for the Gloucester subregion (Frery et al., 2018)). Additionally, the data availability, especially in the surface weathered and fractured rock layer, is too limited to parameterise a complex model or reliably constrain its state variables through observations of head, flux or environmental tracers. The data availability attribute is therefore scored ‘high’.
Developing the regional and alluvial models as separate models at different scales allowed for a focus of efforts and thus required less resources (such as time and computational resources) to develop than would be needed to develop a complex integrated model. The resources column is scored ‘medium’ to reflect that even with more resources available for modelling, an integrated model would not be warranted because of the limited data availability and technical issues.
Recently, the United States Geological Survey published a new version of MODFLOW, MODFLOW-USG (Panday et al., 2015) that allows for grids with spatially varying resolution. At the time of the start of the numerical modelling project in February 2014, this software was not available. While other codes, such as HydroGeoSphere, have that capability and were available, their numerical complexity posed too great a risk in terms of numerical stability and computational resources required for them to be applied in the probabilistic BA framework. The technical column is therefore scored ‘high’ as the above-mentioned technical limitations of the modelling codes available at the start of the modelling project did not allow models with spatially varying grid resolutions.
Notwithstanding the limitations in data and technical issues, the effect on predictions is scored ‘low’. In an integrated model of the deeper basin and the alluvium, there is a two-way interaction between both systems; the groundwater flow in the deeper basin and surface weathered and fractured rock layer will affect the alluvial groundwater flow and in turn, changes in alluvial groundwater will affect the flow in the deeper basin. In the hybrid approach there is only a one-way interaction: changes in groundwater flow in the deeper basin can lead to increases or decreases in the alluvial model in the exchange flux between the alluvial and the weathered zone. Changes in the alluvial model will, however, not lead to changes in the analytic element model. Predictions of change in drawdown or change in flux in the alluvial MODFLOW are therefore not compromised by adopting the hybrid approach. The absence of feedback from the alluvial MODFLOW models to the analytic element models means that drawdowns in the surface weathered and fractured rock layer and deeper sedimentary basin cannot be compensated by increased inflow from the alluvium. This means the drawdowns in the analytic element model are overestimated, which is in line with the precautionary principle.
Principle of superposition
A crucial assumption in the analytic element model is the validity of the principle of superposition, that is, that solutions to the groundwater flow equations are additive as long as the system behaves linearly, as outlined in Section 2.6.2.1. This assumption allows for simulating the change in the system due to coal resource development directly, rather than to simulate all fluxes and stores for two different futures and obtain the change as the difference between those two futures.
The data analysis in companion product 2.1-2.2 for the Gloucester subregion (Frery et al., 2018) highlighted the limited data availability on the current groundwater flow conditions in the surface weathered and fractured rock layer and deeper sedimentary basin. The data attribute is nevertheless scored ‘medium’. The reasoning behind this scoring is that additional data would only warrant to revisit the assumption if the principle of superposition would be shown not to be applicable, that is, if the additional data shows the surface weathered and fractured rock layer and deeper basin do not behave as a confined groundwater system.
The resources and technical attributes are both scored ‘low’ to reflect that this model choice is not driven by operational constraints or technical limitations.
The effect on predictions is scored ‘low’ as Reilly et al. (1987) and Rassam et al. (2004) showed that for mild violations of the linearity assumptions, the deviations in predictions caused by the non-linearity are generally very small and only become apparent in extreme cases.
Horizontally spatially uniform hydraulic properties
The transmissivity (the product of hydraulic conductivity and layer thickness) and storage are considered spatially uniform, at least in the horizontal direction, in both the analytic element model and in the alluvial MODFLOW models.
The limited data available on these hydraulic properties does show that these properties are heterogeneous (companion product 2.1-2.2 for the Gloucester subregion (Frery et al., 2018)). The data density is, however, too limited to empirically establish a spatial correlation structure to characterise the spatial variability in these properties. The sparse head observation dataset does not allow for estimating spatial variability through inverse modelling. The data attribute is therefore scored ‘high’.
Incorporating spatial variability in the modelling would require additional resources as it takes time to develop spatial fields from the available data. In addition to that, incorporating spatial variability will increase the dimensionality of the parameter space. This increases the computational load as more model runs need to be added to the design of experiment to fully explore the larger parameter space. The resources attribute is therefore scored ‘medium’.
In MODFLOW it is trivial to incorporate spatially varying fields. This is less so in the analytic element code, which is not designed to handle spatial variability in hydraulic properties. The technical column is therefore scored ‘medium’.
The effect on prediction is scored ‘low’. Groundwater level and flux estimates, especially at the regional scale, are dominated by the bulk hydraulic properties (Barnett et al., 2012). Companion submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016) illustrates that the probabilistic approach adopted in the BAs ensures that by varying the uniform hydraulic conductivity stochastically, the effects of spatial heterogeneity are captured in the predictive distributions of change in groundwater level. At a local scale, however, within a kilometre of a stress such as an open-pit mine, spatial heterogeneity is important (Crosbie et al., 2016).
Hydraulic properties vary with depth, not with stratigraphy
Most of the sedimentary rocks in the geological Gloucester Basin have a low permeability and no clear correlation between measured hydraulic properties and lithology/stratigraphy is present. In this basin an exponential decrease in depth of the hydraulic properties is, however, observed (Parsons Brinckerhoff, 2015). This warranted the approach of changing hydraulic properties with depth, albeit differently for interburden and coal seams.
The data attribute is scored ‘high’. The data shown in Figure 16 (Section 2.6.2.6.1) on which the depth–hydraulic conductivity relationship is based, are mostly from drill-stem tests and small-scale permeability measurements. Additional data, including pumping tests, are needed to reliably constrain the large-scale hydraulic properties and their variation with lithology and depth.
The choice of varying hydraulic properties with depth is not motivated by operational constraints or technical limitations.
The effect on predictions is scored as ‘medium’. The hydraulic properties of the coal seams control the amount of water that needs to be extracted in CSG wells to achieve the necessary depressurisation and they control the propagation of the cone of depression to the surface weathered and fractured rock layer (Figure 24 and Figure 25). This is mitigated by specifying a wide range for the hydraulic properties, in both the design of experiment (Figure 17 and Figure 22 and the prior parameter distributions (Figure 34), and constraining the prior parameters with a maximum CSG water production rate.
Stochastic representation of coal seams and faults
The coal seams in the Gloucester Basin are difficult to correlate between boreholes because of their heterogeneous deposition and the tectonic history of the basin with the associated faulting. The number and position of coal seams at any location is very difficult to predict. Likewise, the number, throw and orientation of faults, especially subseismic faults, are nearly impossible to assess deterministically. The stochastic representation of number and position of coal seams and of the position and extent of faults allows capture of, at least at a basic level, the compartmentalisation of the sedimentary basin. In this conceptualisation, faults act as horizontal barriers and vertical conduits.
The data attribute is scored ‘high’. Additional seismic data and borehole information will undoubtedly reduce the uncertainty in the position and extent of the major faults. The stochastic generation of subseismic faults in the analytic element model is mostly based on international datasets of fault geometry. Additional data, such as high resolution seismic data, is needed to validate and improve the stochastic fault generation.
Resources are scored ‘low’. A considerable amount of the available resources in the project is invested in developing the geological model (companion product 2.1-2.2 for the Gloucester subregion (Frery et al., 2018)) to gain insight in the position and extent of faults and in integrating that information in the numerical model stochastically to ensure the available information is used to its fullest extent.
The technical attribute is likewise scored ‘low’. One of the main reasons for selecting the analytic element method was the capability to represent linear features stochastically, which is not straightforward in codes such as MODFLOW. Note that MODFLOW-USG provides enhanced functionality to represent linear features.
Throughout the parameterisation of the faults, the precautionary principle is applied by favouring parameter combinations in which faults act as vertical conduits and horizontal barriers. While there is little evidence in observations for this hydraulic fault behaviour, it will result in maximum propagation of the depressurisation in the coal seams to the surface weathered and fractured rock layer. The stochastic approach means that while no individual realisation and resulting predictions will accurately reflect the field conditions, a very wide range of potential fault distributions are incorporated in the numerical modelling. Despite the density of faults and their parameterisation, the drawdown predictions in the surface weathered and fractured rock layer were not very sensitive to any of the fault parameters (Figure 25 and Figure 26), which is why the effect on predictions attribute is scored ‘low’.
Random location of coal seam gas wells and assigning pumping interval to random coal seams
At the time of defining the CRDP, the exact location and target coal seams for the AGL Stage 1 gas field development were not available. 110 CSG wells are located in the analytic element model through a random process that adheres to the implementation plan outlined by AGL in Parsons Brinckerhoff (2015).
The data attribute is scored ‘high’ as the exact locations are not known. The resources and technical attributes are scored ‘low’ as it is trivial to change the location of CSG wells in the analytic element model.
The effect on predictions is scored ‘low’. While the random realisation of well locations and coal seams pumped will, in all probability, not correspond to the wellfield that will potentially eventuate, the density of wells ensures that the simulated effect will at least be comparable in size of impact.
Coal seam gas wells as constant head wells
The amount of water extracted from CSG wells is a function of the gas content and the coal permeability. As such it is difficult to predict at the regional scale with a single phase model. Specifying CSG wells as head-dependent boundaries allows for the extraction rate to vary with hydraulic properties.
The data attribute is once more scored ‘high’ as the exact water extraction rates are not known.
The technical attribute is scored ‘high’ as most groundwater model codes, including TTim and MODFLOW, are not able to simulate dual-phase flow. Using a single-phase model is, however, likely to overestimate drawdowns and water extraction volumes (Herckenrath et al., 2015), in line with the precautionary principle. The codes do allow for specifying pumping rates, but these are not known and, because of the dual phase aspect, will be unlikely to result in a drawdown that is representative of the depressurisation required for CSG extraction (see submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016)).
As the pumping rate is the main CSG-related stress on the system, its magnitude is very important and can greatly affect the predictions. The effect is partly mitigated by biasing the prior parameter combinations in favour of combinations that lead to elevated water extraction rates, while simultaneously constraining the parameters with an upper limit to the extraction rates. This process avoids both unrealistically high and unrealistically low extraction rates.
The spatial patterns of drawdown in the surface weathered and fractured rock layer (Figure 37) are heavily influenced by the mine footprints. Any spatial patterns linked to the location of the CSG wells is hard to distinguish. This is to be expected as the pumping rates assigned to the mines (Figure 15) are almost an order of magnitude larger than the maximum CSG water production rates.
The effect on predictions is therefore scored ‘medium’.
Open-cut mines as prescribed pumping rate
Pumping rates to dewater open-cut coal mines depend largely on local conditions. As local conditions are not well captured in the GW AEM, the choice was made to use reported historical or locally modelled extraction rates in the model.
The data attribute is scored ‘high’. To implement open-pit mine dewatering it is essential to know the exact elevation of the mine dewatering level as well as the proposed dewatering scheme. This information is beyond the spatial resolution of the geological model.
The resources and technical attributes are scored ‘low’ as it is trivial to specify the mine pit dewatering as head-dependent flux boundary conditions and it does not appreciably increase the computational demand or processing time.
The effect on predictions is scored ‘high’ as a change in pumping rate will greatly affect predictions, and the reliability of the predictions of this model hinge on the quality of the pumping rates reported by the mining companies. The prescribed pumping rates are at least consistent with the modelling done by the mining companies which incorporates a large amount of local detail on the geology and mine planning that is beyond the resolution of the BA modelling.
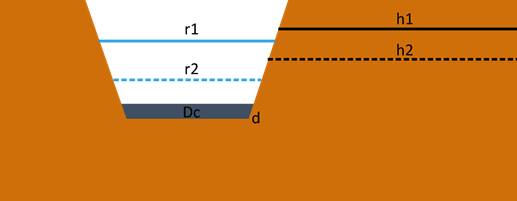
River network implemented as drainage boundary
The river network in the alluvial MODFLOW models implemented a drainage boundary condition, which is a boundary condition that only allows water to leave the groundwater system. The RIVER package in MODFLOW allows for two-way surface water – groundwater interaction.
The data attribute is scored ‘high’. To implement the drainage boundary, it suffices to specify a drainbed elevation and drainbed conductance. The drainbed elevation can be estimated from a high resolution digital elevation model. For a river boundary, the river stage needs to be specified as well. The limited availability of gauging stations in the Gloucester subregion requires that river stages be interpolated over large distances. The specification of river stage in the future is even more problematic as it requires converting the simulated streamflow predictions of the Australian Water Resource Assessment Landscape module (AWRA-L) to river stages using a rating curve. Rating curves are not constant in time and are known to have large uncertainties, especially for low-flow conditions (Tomkins, 2014). The data requirements to implement a river boundary are much higher and will introduce considerable additional uncertainty.
The resources and technical attributes are scored ‘low’ as it is straightforward to implement a river boundary in MODFLOW and the effect on runtime and processing is negligible.
h1 = groundwater level before coal resource development; h2 = groundwater level after coal resource development; r1 = river stage before coal resource development; r2 = river stage after coal resource development; d = drainbed elevation; Dc = conductance
The effect on predictions is scored ‘low’. Drawdowns in the alluvium will be overestimated as the drainage boundary does not allow drawdown to be compensated by induced inflow from the river. As long as the river system is connected and the groundwater level is above the drainbed conductance, the drain boundary condition will ensure that the change in flux due to coal resource development is overestimated under both gaining and losing conditions. This is illustrated in Figure 42. The change in flux estimated with a river boundary condition ![]() is equal to:
is equal to:
|
|
(17) |
where h1 is groundwater level before coal resource development; h2 is groundwater level after coal resource development; r1 is river stage before coal resource development; r2 is river stage after coal resource development; and Dc is conductance.
The change in flux estimated with a drainage boundary condition ![]() can be written as:
can be written as:
|
|
(18) |
where d is drainbed elevation. The change in flux computed with a drain boundary condition will therefore always be larger than the flux computed with a river boundary condition, as long as the river stage after coal resource development (r2) is equal to or smaller than the river stage before coal resource development (r1). This condition is always satisfied in the numerical modelling of the impact of coal resource development on surface water.
The equations above are only valid as long as the groundwater levels are above the drainbed elevation. The probability maps of exceeding 0.2 m drawdown in the alluvium (Figure 40) show that these conditions only occur very locally.
Constrain model with flux estimates rather than head observations
Traditionally, groundwater models are evaluated based on the agreement of observed head observations and their simulated equivalent. In this modelling exercise, head observations are not formally used to constrain the model; only water balance estimates are used. Water balance estimates are chosen because they represent a spatially and temporally integrated estimate of the state variables and are therefore more robust to constrain spatially uniform parameters in the MODFLOW models.
This assumption is mostly driven by data availability and scores ‘high’ on this attribute. The data density of groundwater level observations is considered too low to reliably constrain the uniform hydraulic properties and boundary conditions.
The resources attribute is scored ‘low’ as constraining the model with additional observations would not require additional resources.
The technical attribute is scored ‘low’ as well as the uncertainty workflow is able to integrate head observation. An example of integrating groundwater level observation in the BA uncertainty analysis workflow can be found in companion product 2.5 for the Clarence-Moreton bioregion (Cui et al., 2016).
The effect on predictions of integrating head observation is considered to be small and therefore the attribute receives a ‘low’ score. The predictions of drawdown are most sensitive to the hydraulic properties in the weathered zone, both in the MODFLOW model and the analytic element model (Figure 32). The water balance estimates are not able to greatly constrain these parameters (Figure 36). Groundwater level observations in the alluvium are mostly affected by local conditions, such as river stage, recharge and local hydraulic properties. It is unlikely that such observations contain enough information to constrain the hydraulic properties relevant to the maximum additional drawdown predictions as is illustrated in the uncertainty analysis of the Clarence-Moreton bioregion groundwater model (see companion product 2.5 for the Clarence-Moreton bioregion (Cui et al., 2016)).
Specification of prior parameter distributions
The specification of prior distributions is of great importance in any uncertainty analysis. The process to specify the prior distributions is outlined in Section 2.6.2.8.1.1.
Once more, the data attribute is scored ‘high’, reflecting the limited data availability in the region. Due to operational constraints, it was not possible to organise an elicitation workshop with local experts to establish the prior distributions. The resources attribute is therefore scored ‘medium’.
The technical column is scored ‘low’ as the uncertainty analysis methodology allows to specify a wide variety of prior distributions.
The effect on predictions is scored ‘medium’ as there is limited data available to constrain the prior distributions, especially the distributions of the parameters the predictions are most sensitive to. The effect is mitigated by specifying prior distributions with a high variance, in the case of hydraulic properties to cover at least one order of magnitude. This is likely to represent a conservative estimate of the actual parameter distributions.
Simulation period from 2012 to 2102
Across the Bioregional Assessment Programme, the simulation period is chosen to be from 2012 to 2102 as discussed in companion submethodology M06 (as listed in Table 1) for surface water modelling (Viney, 2016) and companion submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016). For some parameter combinations and some receptors this means that the maximum drawdown is not realised within the simulation period, as shown in Figure 20, Figure 38 and Figure 39.
Extending the simulation period is not limited by data as it is about the future, hence the score ‘low’. The resources attribute is, however, scored ‘high’. To ensure that the maximum drawdown is realised at all receptor locations for all parameter combinations, would require extending the simulation period with hundreds to even thousands of years. This would impose a sizeable increase in the computational demand and therefore compromise the comprehensive probabilistic assessment of predictions. The technical attribute is scored ‘medium’. It is trivial to extend the simulation period in both the analytic element model and the MODFLOW model. The climate scaling factors used to specify future rainfall and therefore recharge are not available beyond 2100. It is therefore a technical issue in devising a justifiable future climate to assign to the modelling.
The effect on predictions, however, is scored ‘low’. Figure 39 indicates that the maximum drawdown decreases with increasing time to maximum drawdown. This is in line with the theoretical assessment of the relationship between dmax and tmax presented in submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016). It can be shown that any drawdown due to additional coal resource development realised after 2102, will always be smaller than the drawdowns realised before 2102. This is in line with the precautionary principle as it means that by limiting the simulation period, the hydrological change will not be underestimated.
Product Finalisation date
- 2.6.2.1 Methods
- 2.6.2.2 Review of existing models
- 2.6.2.3 Model development
- 2.6.2.4 Boundary and initial conditions
- 2.6.2.5 Implementation of coal resource development pathway
- 2.6.2.6 Parameterisation
- 2.6.2.7 Observations and predictions
- 2.6.2.8 Uncertainty analysis
- 2.6.2.9 Limitations and conclusions
- Citation
- Acknowledgements
- Currency of scientific results
- Contributors to the Technical Programme
- About this technical product