The purpose of a statistical emulator is to provide a computationally efficient surrogate for a computationally expensive model. These emulators provide a way to quantify the predictive distribution for a prediction of interest, given a new set of parameters at which the model was not run. The statistical emulation approach employed herein is called Local Approximate Gaussian Processes (LAGPs) as implemented through the ‘aGP’ function of the ‘laGP’ package (Gramacy, 2014) for R (R Core Team, 2013). LAGPs were chosen because: (i) they can be built and run very rapidly in the ‘laGP’ R package; (ii) unlike some other popular emulation approaches (e.g. standard Gaussian process emulators), they allow for nonstationarity in the model output across the parameter space which provides the emulator with more flexibility to match model output; and (iii) they were found to have excellent performance when compared to a range of other emulation techniques (Nguyen-Tuong et al., 2009; Gramacy, 2014).
The training and evaluating of an individual emulator is implemented through a set of custom made R-scripts with following input requirements:
- design of experiment parameter combinations
- design of experiment model output
- transform of parameters
- transform of output.
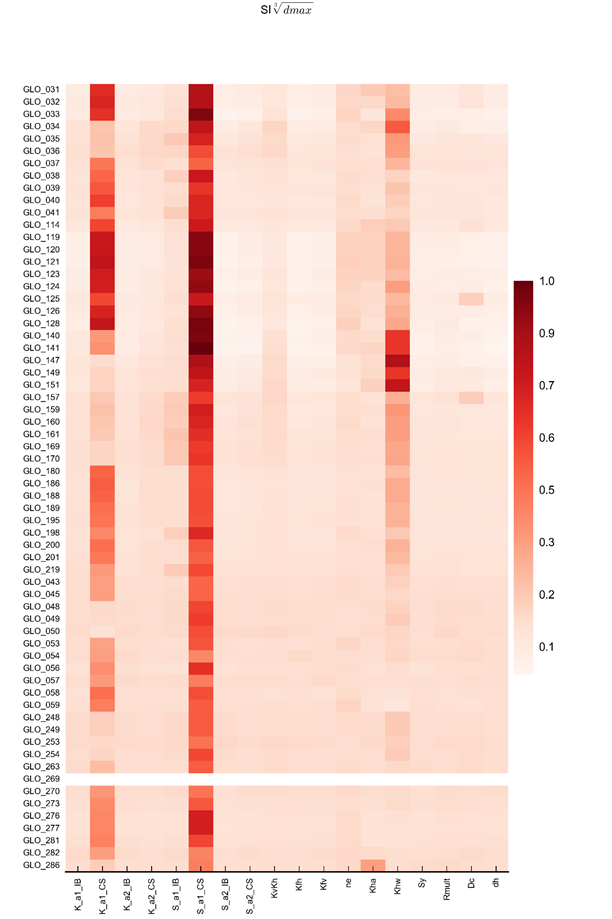
In constructing the emulators for drawdown at the receptor locations, cubed-root transforms of the model outputs were used, while the emulators for year of maximum change were trained on untransformed model outputs. The design of experiment model parameters were either used in their natural forms (i.e. parameters K_IB_slope, K_CS_slope, S_IB_slope and S_CS_slope) or log10-transformed (i.e. K_IB_intercept, K_CS_intercept, S_IB_intercept, S_CS_intercept, KvKh, Kfh, Kfv and ne) depending upon the range sampled in the design of experiment.
When evaluating a trained LAGP emulator for a new parameter combination, the emulator provides a mean and standard deviation of the prediction the emulator is trained for. The mean can be considered the best estimate of the prediction value corresponding to the new parameter combination, while the standard deviation provides as estimate of the uncertainty related to using the emulator.
Refer to Table 5 in Section 2.6.2.6.1 for definitions of terms.
Data: Bioregional Assessment Programme (Dataset 5)
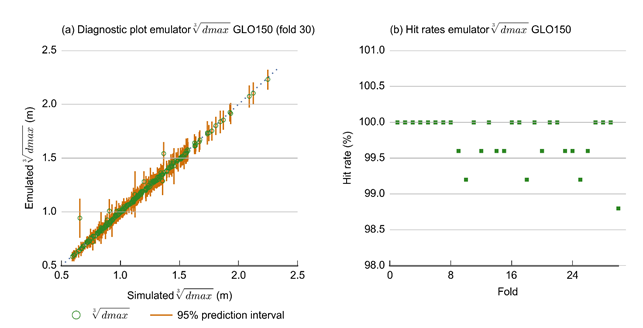
The predictive capability of an LAGP emulator is assessed via 30-fold cross validation (i.e. leaving out 1/30th of the model runs, over 30 tests) and recording diagnostic plots of the emulator’s predictive capacity. For each of the 30 runs of the cross-validation procedure, the proportion of 95% predictive distributions that contained the actual values output by the model (also called the hit rate) was recorded. These plots were verified to ensure that close to 95% of values were contained in these intervals. Figure 33(a) and Figure 33(b) show two examples of these plots for the dmax values of receptor GLO_150. The blue dotted line in Figure 33(a) shows the 1:1 line and the orange lines show the 95% predictive intervals from the LAGP emulator. The points plotted in Figure 33(b) show the hit rates achieved by the emulator in each of the 30 folds of cross validation used. These are all well above the target of 95%.
Data: Bioregional Assessment Programme (Dataset 1)
When the emulator is used to evaluate a new parameter combination in the Monte Carlo step of the uncertainty analysis (Figure 6 in Section 2.6.2.1), a random sample is generated from the normal distribution defined by the mean and standard deviation of the emulator output. Only emulators with a hit rate in excess of 95% are used in the Monte Carlo analysis. This ensures that the emulator results are true to the original model output and that the predictive uncertainty is overestimated, rather than underestimated.
For some receptors it will not be possible to create an emulator with sufficient precision and it will not be possible to adequately estimate the predictive posterior ensemble for those. These receptors are labelled as such in Dataset 2 (Bioregional Assessment Programme, Dataset 2) and the median of the design of experiment is used as their predicted value.
Product Finalisation date
- 2.6.2.1 Methods
- 2.6.2.2 Review of existing models
- 2.6.2.3 Model development
- 2.6.2.4 Boundary and initial conditions
- 2.6.2.5 Implementation of coal resource development pathway
- 2.6.2.6 Parameterisation
- 2.6.2.7 Observations and predictions
- 2.6.2.8 Uncertainty analysis
- 2.6.2.9 Limitations and conclusions
- Citation
- Acknowledgements
- Currency of scientific results
- Contributors to the Technical Programme
- About this technical product