2.6.2.4.2.1 Recharge
Rainfall recharge is spatially and temporally varying, reflecting spatial differences in geology and temporal variation in rainfall. The derivation of a mean annual recharge surface for the Hunter subregion using a chloride mass balance approach is described in Section 2.1.3 of companion product 2.1-2.2 for the Hunter subregion (Herron et al., 2018). The long-term temporal variation of rainfall is described in Section 1.1.2 of the Hunter context statement (companion product 1.1 (McVicar et al., 2015)). This is normalised so its average throughout the period 1983 to 2012 is one, and the resultant time series is multiplied by the spatial variation to yield the final recharge applied to the model. Recharge is applied as a source of water of prescribed rate to the land surface of the model. To account for uncertainties in both the temporal and spatial variation of recharge, its magnitude is varied in the uncertainty analysis (see companion submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016)).
2.6.2.4.2.2 Evapotranspiration
Evapotranspiration is represented by a sink of groundwater applied across the entire land surface of the model, excluding the parts under the ocean. Generally in groundwater models, evapotranspiration from groundwater is assumed to be maximum when the phreatic surface is close to the ground surface, or above it (e.g. in the case of ponding). This gives rise to the so-called ‘potential evapotranspiration’, PET, which is the maximum possible rate of evapotranspiration. PET is temporally and spatially varying, PET = PET(x,y,t), which reflects seasonal changes, and different vegetation and surface expression of geology. Conversely, evapotranspiration from groundwater is generally assumed to be zero when the phreatic surface is deep below the ground surface since plant roots cannot draw water from the deep groundwater reserves. This gives rise to the so-called ‘extinction depth’, d, which parameterises the depth of plant roots. Clearly d depends on the type of vegetation, as discussed below. When the phreatic surface is somewhere between the extinction depth and the ground surface, evapotranspiration is a fraction of PET.
The Hunter groundwater model uses the daily PET time series produced by the Australian Water Resource Assessment landscape (AWRA-L) model (Bioregional Assessment Programme, Dataset 6), which was based on one particular future climate scenario (See Section 2.6.1.3 in companion product 2.6.1 for the Hunter subregion (Zhang et al., 2018)). The groundwater model is run using monthly time steps. Appropriate averaging of the daily PET time series provides data that can be used in the groundwater model, and this is conveniently represented by:
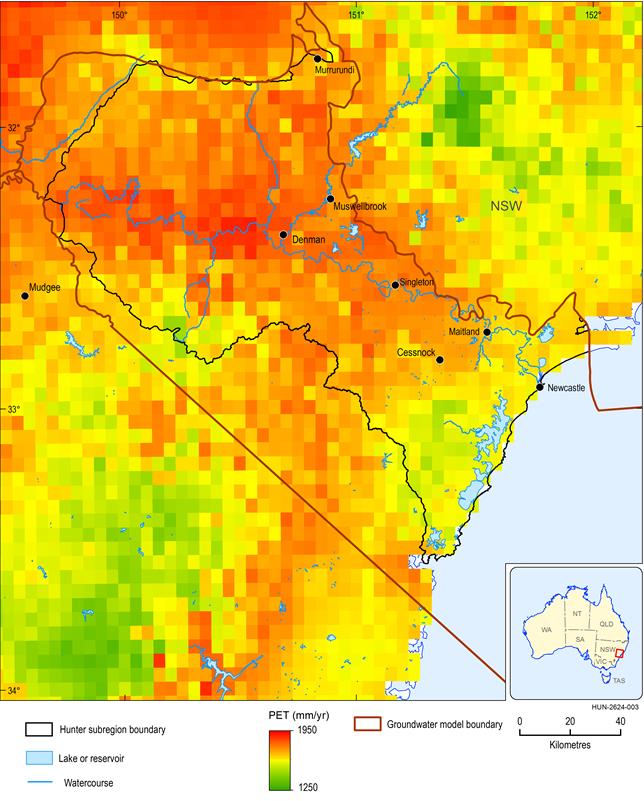
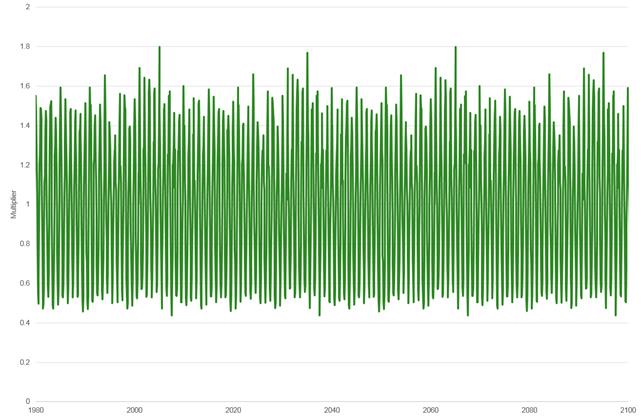
To obtain the PET at a location and a specific month, the PET of the appropriate pixel shown in Figure 13 is multiplied by the temporal factor of Figure 14.
Figure 13 Spatial variation of potential evapotranspiration (PET) from AWRA-L
Data: Bioregional Assessment Programme (Dataset 6)
Figure 14 Temporal multiplier for potential evapotranspiration (PET) in the groundwater model
Data: Bioregional Assessment Programme (Dataset 6)
Generally in groundwater models the extinction depth, d, is set between 0 m (zero vegetation) and 20 m (deep rooted trees) with a value of 5 m being typical (Doble and Crosbie, 2016). In the Hunter groundwater model d varies between 0 m and 10 m. It is assumed that d is proportional to vegetation height, V, with the rationale being that taller trees typically have deeper roots than smaller shrubs or grasses (Canadell et al., 1996). Vegetation height is quantified in Figure 18 of companion product 1.1 for the Hunter subregion (McVicar et al., 2015) and details of the vegetation height dataset (Caltech/JPL, Dataset 7) can be found in Section 2.1.1 of companion product 2.1-2.2 for the Hunter subregion (Herron et al., 2018). Since it varies between 0 m and 39 m throughout the subregion, the groundwater model uses:
|
|
(2) |
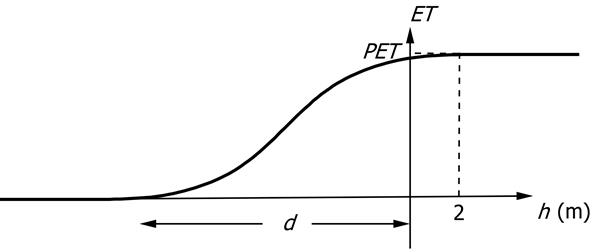
At any point on the surface of the Hunter groundwater model, evapotranspiration varies as a cubic function of groundwater head, h, at that point, as shown in Figure 15. When h is high (the groundwater level is above the topography) ET = PET, but when h is low (the groundwater level is well below the topography) ET = 0. The transition from the cubic to PET is chosen to be at h = 2 m. If this transition was chosen to be at h = 0, as is common, and a point happened to have d = 0 (which is quite common when using the vegetation height to define d), the numerical solver may only slowly converge to the solution for groundwater levels due to the sudden transition from PET to zero.
ET = PET for h>2 m as indicated by the dashed lines.
Product Finalisation date
- 2.6.2.1 Methods
- 2.6.2.2 Review of existing models
- 2.6.2.3 Model development
- 2.6.2.4 Boundary and initial conditions
- 2.6.2.5 Implementation of the coal resource development pathway
- 2.6.2.6 Parameterisation
- 2.6.2.7 Observations and predictions
- 2.6.2.8 Uncertainty analysis
- 2.6.2.9 Limitations and conclusions
- Citation
- Acknowledgements
- Currency of scientific results
- Contributors to the Technical Programme
- About this technical product