2.6.2.7.3.1 Stress testing of the groundwater model
As outlined in Section 2.6.2.1, the groundwater model is evaluated for a wide range of parameter combinations chosen in a systematic and efficient way. The first stage of this evaluation applied a stress test to evaluate the stability of the model when run using a wide range of parameters. The stress testing involved undertaking 100 model runs. This exercise also helped to identify the minimum and maximum of the range of parameters for the design of experiments that can result in better model stability while ensuring that sampling from within this range explores the full range of predictive uncertainty. Further, it helped in identifying parameters that did not affect the model predictions. Based on the outcomes of the stress test, model parameterisation is further reviewed to either remove the parameters that did not affect the predictions or tie these parameters to other independent parameters.
The stress testing of the Namoi subregion groundwater model revealed that many of the 81 parameters chosen for the initial parameterisation of the model contained insensitive parameters and that a parameterisation scheme with 37 independent parameters is sufficient to comprehensively explore model sensitivity to parameters (parameters are listed as free or tied in Table 10 of Section 2.6.2.6). The stress testing informed that it is not critical to parameterise each interburden layer with a separate parameter for its hydraulic properties at zero depth (e.g. IB_K0). Instead, the same parameter could be used for all the nine numerical model layers corresponding to the three interburden layers. Despite using the same parameter value, the depth-based decay of hydraulic properties ensures that all the nine interburden layers assume distinct values of hydraulic properties.
Subsequent to the stress testing, the groundwater model is evaluated for a wide range of parameter combinations chosen in a systematic and efficient way that is referred to as the design of experiment (see companion submethodology M09 (as listed in Table 1) for propagating uncertainty through models (Peeters et al., 2016)). The results of these model runs, the simulated equivalents to the observations described in Section 2.6.2.7.1 and the predictions described in Section 2.6.2.7.2, are used for the sensitivity analysis. In the uncertainty analysis the results are filtered and only the runs that are consistent with the observations are retained (see Section 2.6.2.8.1). Each parameter is sampled across a wide range to ensure sufficient coverage of the parameter space. The design-of-experiment model runs also allow a comprehensive sensitivity analysis to be undertaken. Such an analysis provides insight into the functioning of the model and aids in identifying which parameters the predictions are most sensitive to and if the observations are able to constrain these parameters.
Table 10 in Section 2.6.2.6 lists the 81 parameters in the model and identifies the 37 that were varied in the sensitivity and uncertainty analyses and how they relate to the hydraulic properties, stresses and boundary conditions of the groundwater model. The ‘Description’ column provides a plain-English description of the parameters. The ‘Note’ column identifies which parameters were fixed and also whether they have been sampled after being log-transformed. The ‘Minimum’ and ‘Maximum’ columns provide the range over which the parameter is sampled. Not all the model parameters were carried through to the sensitivity and uncertainty analyses. Rationalising the number of parameters was undertaken to reduce the total number of simulations needed to characterise modelling uncertainty. Where a number of parameters are used to define a process in the model, it is possible to fix some and vary others to obtain a satisfactory characterisation of the range of possible outcomes. The parameters relating to the general-head boundary conductance, the riverbed conductance and evapotranspiration are not included in the uncertainty analysis as initial model runs indicated that these parameters have a very limited effect on predictions.
Using a maximin Latin Hypercube design (see Santner et al., 2003, p. 138), 3500 parameter combinations were generated for the entire parameter space for the groundwater model. The maximin Latin Hypercube design is generated like a standard Latin Hypercube design, one design point at a time, but with each new point selected to maximise the minimum Euclidean distance between design points in the parameter space. Points in the design span the full range of parameter values in each dimension of the parameter space, but also avoid redundancy among points by maximising the Euclidean distance between two points (since nearby points are likely to have similar model output). The parameter ranges are sampled uniformly from their range.
Of the 3500 parameter combinations, 2618 resulted in successful runs of the model that produced all the required outputs. Within the available time frame and with the available computational resources, the modelling team was able to successfully evaluate 2618 parameter combinations. Although the coverage of a 37-dimensional parameter space is limited with 2618 simulations, visual inspection of the parameter combinations evaluated showed that there was no bias or gaps in the sampling of the parameter hyperspace.
The following sections describe the sensitivity of the observations and predictions to the 37 parameters, based on these model runs.
2.6.2.7.3.2 Simulated equivalents to observations from the design of experiment
The best appreciation of the relationship between a parameter and an observation or prediction is through the inspection of scatter plots. The large dimensionality of parameters, observations and predictions precludes this type of visualisation for all parameter–prediction combinations, so a few scatter plots are provided as illustration. A comprehensive assessment of sensitivity is provided through sensitivity indices. These indices, computed using the methodology outlined in Plischke et al. (2013), are a density rather than variance-based quantification of the change in a prediction or observation due to a change in a parameter value. It is a relative metric in which large values indicate high sensitivity, whereas low values indicate low sensitivity. The indices are normalised by the largest sensitivity index, such that the most sensitive parameter has an index value of 1.
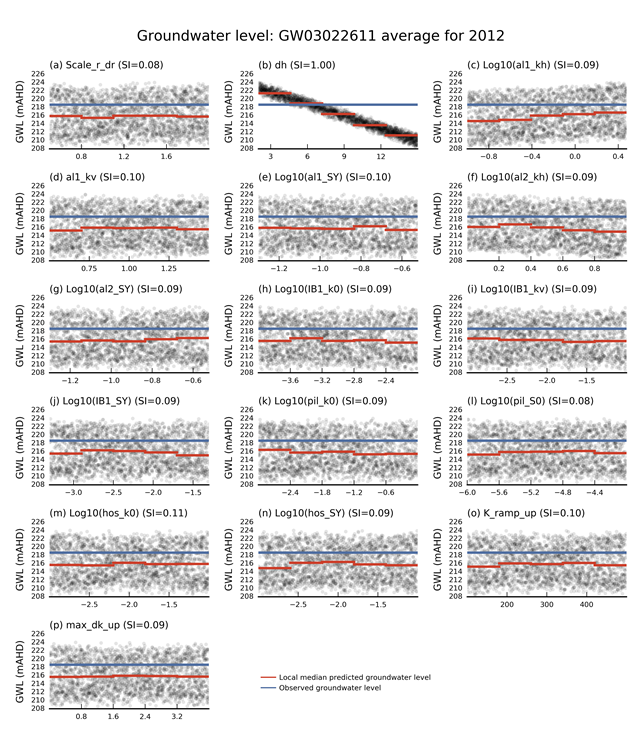
Figure 23 shows how the average predicted groundwater levels at observation bore GW030226.1.1 in 2012 vary with parameter values. The sensitivity index for each parameter is also shown. The blue line indicates the observed groundwater level. It is clear that there are parameter combinations that can match the observed value of the average groundwater level in 2012 but the variation in the prediction is completely dominated by a single parameter, dh, the depth of incision of the streambed below topography. This demonstrates that this particular observation is not sensitive to other parameters such as recharge or hydraulic conductivity that would ordinarily have an influence over the groundwater level; the reason for this is that the location of this particular observation bore is close to the river and therefore is controlled by the elevation of the water in the river.
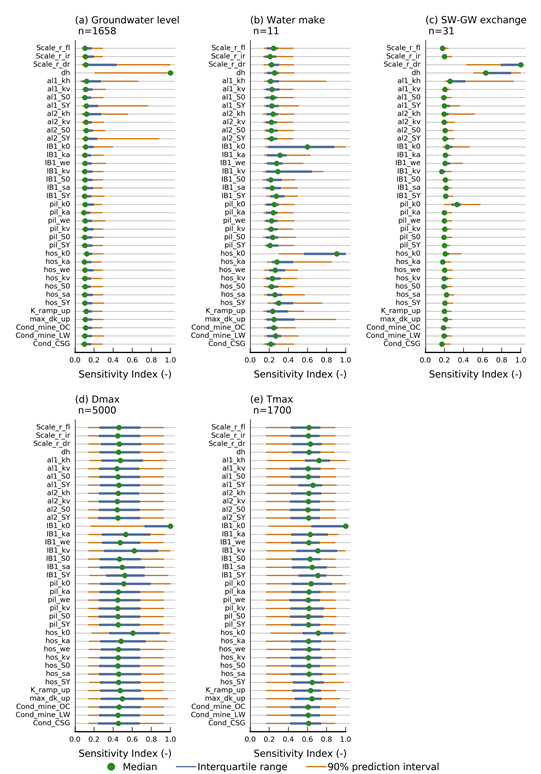
Figure 24a shows boxplots of the sensitivity indices for all available simulated equivalents to groundwater level observations. As with observation bore GW030226.1.1, the depth of incision of the streambed (dh) is the most influential parameter across all groundwater level observations but there are also some observations that are sensitive to the scaler applied to diffuse recharge (Scale_r_dr) and the hydraulic properties of the alluvium (al1_kh, al1_SY, al2_kh and al2_SY). The relative insensitivity of groundwater level predictions to the other parameters does not mean these variables have no effect; rather it indicates the effect of these parameters is small compared to other parameters and is too small to be distinguished based on a design of experiment with 2618 evaluated parameter combinations.
The blue line is the observed groundwater level and the red lines are the median of the predicted water level binned over a quintile of the parameter space.
GWL = groundwater level; mAHD = metres above the Australian Height Datum; SI = sensitivity index; parameter names are described in Table 10.
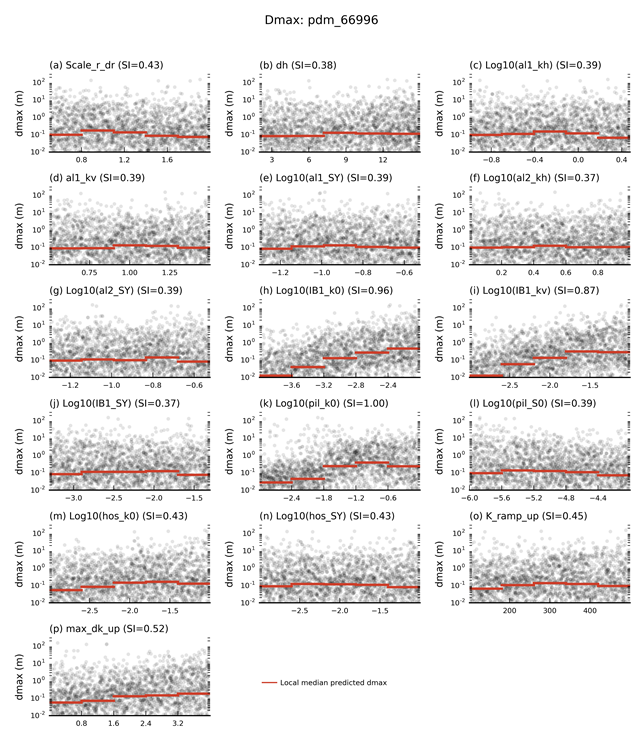
Additional drawdown is the maximum difference in drawdown (dmax) between the coal resource development pathway (CRDP) and baseline, due to additional coal resource development.
For those parameters that do not seem to have an inter-quartile range, the range is narrower than the size of the green dot indicating the median
SW = surface water; GW = groundwater; n = the number of observations, parameter names are described in Table 10.
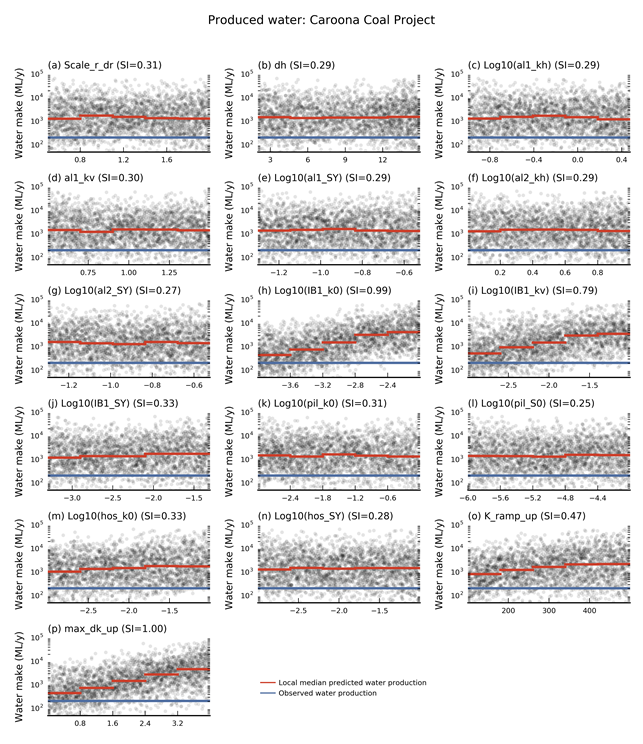
Figure 25 shows scatter plots of the parameter values versus the simulated mine water make for the proposed underground mine at the Caroona Coal Project for all of the evaluated design-of-experiment model runs. The most sensitive parameters are the hydraulic conductivity enhancement after the longwall panels collapse (max_dk_up) and the horizontal and vertical hydraulic conductivities of the interburden (IB1_k0, IB1_kv). This shows that with increasing hydraulic conductivity (either native or enhanced) there is an increase in mine water make. Figure 24b shows that the other mines behave similarly with the hydraulic conductivity enhancement (max_dk_up) being influential for the longwall mines and the hydraulic properties of the coal-bearing units (hos_k0, hos_ka and hos_SY) and interburden (IB1_k0 and IB1_kv) also being influential. The sensitivity of simulated mine water makes to the other parameters is small (i.e. beyond the resolution of the design of experiment).
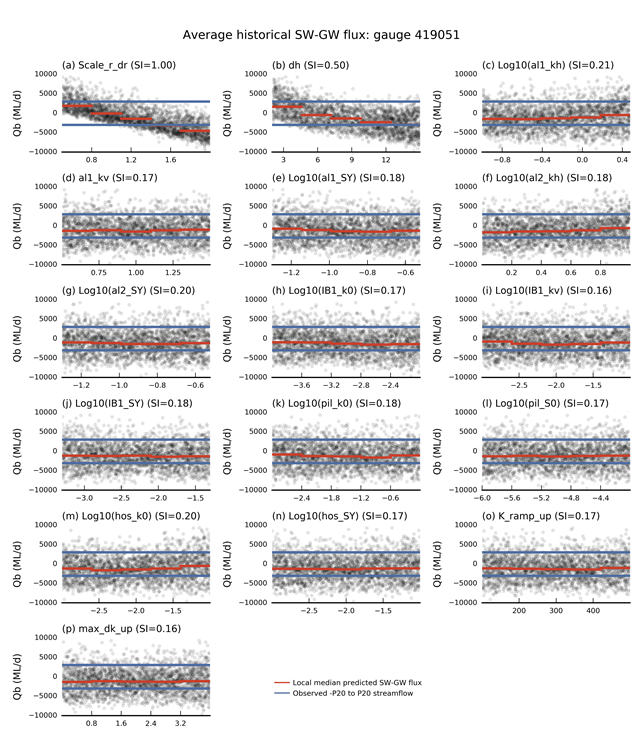
Figure 26 shows scatter plots of the parameter values versus the simulated average historical surface water – groundwater flux at gauge location 419051 for all of the evaluated design-of-experiment model runs. The most sensitive parameters are the scaler applied to diffuse recharge (Scale_r_dr) and the depth of incision of the streambed below topography (dh). This shows that as recharge increases, the surface water – groundwater flux becomes more negative (i.e. groundwater leaving the model domain as discharge to surface water); the converse is also true with low recharge the flux direction is reversed and the river loses water to groundwater. Similarly with the depth of incision of the streambed, a shallow streambed incision results in a losing stream while a deep incision leads to a gaining stream. Figure 24c confirms that these parameters are influential for the other gauge locations as well along with the hydraulic conductivity of the alluvium (al1_kh). As for the other model outputs, the effect of other parameters on surface water – groundwater flux is too small to be distinguished with the current set of model runs.
The blue line is the mine water make reported for the Caroona Coal Project as part of their environmental impact statement (EIS) and the red lines are the median of the simulated mine water make binned over a quintile of the parameter space.
SI = sensitivity index; parameter names are described in Table 10.
The blue lines are ±20% of the average daily flow past the gauge and the red lines are the median of the simulated surface water –groundwater flux upstream of the gauge binned over a quintile of the parameter space.
SW = surface water; GW = groundwater; SI = sensitivity index; parameter names are described in Table 10.
2.6.2.7.3.3 Drawdown predictions (dmax) and year of maximum change (tmax)
Figure 27 shows scatter plots of the parameter values versus predicted maximum difference in drawdown (dmax) at model node 66996 for all evaluated design-of-experiment model runs. This model node is located close to the Narrabri North and Narrabri South mines and the Narrabri CSG Project. The most sensitive parameters for the drawdown prediction at this location are the hydraulic conductivity of the layer that it is located in (pil_k0), the hydraulic properties of the interburden (IB1_k0 and IB1_kv) and the hydraulic conductivity enhancement after longwall mine collapse (max_dk_up). These parameters all show that higher conductivity leads to higher drawdown. Figure 24d shows that across all model nodes it is the hydraulic properties of the interburden, the coal-bearing units and the Pilliga Sandstone that are the most influential. The hydraulic enhancement after longwall mine collapse is not very influential across all model nodes because there are only three longwall mines compared to 10 open-cut mines. The relative insensitivity of drawdown to the other parameters does not mean these variables have no effect; rather it indicates the effect of these parameters is small compared to other parameters and is too small to be distinguished based on the number of samples in this design of experiment.
SI = sensitivity index; parameter names are described in Table 10.
