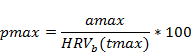- Home
- Assessments
- Bioregional Assessment Program
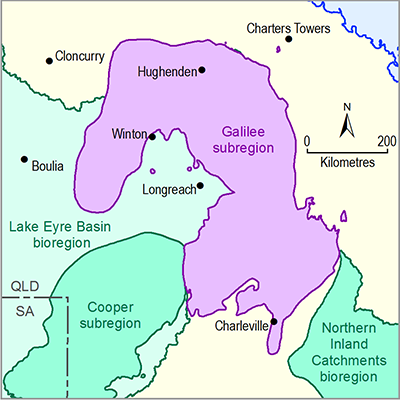
- Galilee subregion
- 2.6.1 Surface water numerical modelling for the Galilee subregion
- 2.6.1.5 Uncertainty
- 2.6.1.5.1 Quantitative uncertainty analysis
The aim of the quantitative uncertainty analysis is to provide a probabilistic estimate of the change in the hydrological response variables due to coal resource development at the model nodes. A large number of parameter combinations are evaluated and, in line with the Approximate Bayesian Computation outlined in companion submethodology M09 (as listed in Table 1) for propagating uncertainty through models (Peeters et al., 2016), only those parameter combinations that result in acceptable model behaviour are accepted in the parameter ensemble used to make predictions.
Acceptable model behaviour is defined for each hydrological response variable based on the capability of the model to reproduce observed time series of the hydrological response variable. For each hydrological variable, a goodness of fit between model simulated and observed annual hydrological response variable is defined and an acceptance threshold defined.
The ensemble of predictions are the changes in hydrological response variable simulated with the parameter combinations for which the goodness of fit exceeds the acceptance threshold. The resulting ensembles are presented and discussed in Section 2.6.1.6.
2.6.1.5.1.1 Design of experiment
The parameters included in the uncertainty analysis are the same as those used in the calibration, with the exception that in the uncertainty analysis parameter ne_scale is included. Table 7 lists the parameters used in the uncertainty analysis, the range and distribution type sampled in the design of experiment and the transformation of the parameter. The Australian Water Resources Assessment landscape model (AWRA-L) parameters in Table 7 are explained in the AWRA-L v4.5 documentation (Viney et al., 2015).
Table 7 AWRA-L parameters included in the quantitative uncertainty analysis
AWRA-L = Australian Water Resources Assessment landscape model, na = data not applicable
Through a space-filling Latin Hypercube sampling (Santer et al., 2003), 10,000 parameter combinations are generated from the AWRA-L parameters, with the ranges and transformations shown in Table 7. These ranges and transformations are chosen by the modelling team based on previous experience in regional and continental calibration of AWRA-L (Vaze et al., 2013). These mostly correspond to the upper and lower limits of each parameter during calibration.
Each of the 10,000 parameter sets is used to drive AWRA-L to generate streamflow time series at each 0.05 x 0.05 degrees grid cell.
2.6.1.5.1.2 Observations
For eight of the nodes in the model domain, observations of streamflow are available. For these catchments the historical observations of streamflow are summarised into the eight hydrological response variables (daily flow at the 1st percentile (P01) is not used) for all years with a full observational record. The equivalent historical simulated hydrological response variable values are computed from the 10,000 design of experiment runs.
Preliminary runs revealed that some parameter sets result in the effect of the 2010–2011 floods on the low-flow part of the hydrograph to persist for up to 25 years after the flooding. This in turn results in the counter-intuitive and unrealistic artefact that even under a drying climate the flow rates in dry periods increase. As the extreme 2010–2011 floods happen late in the observation record, the available observations are not able to constrain the AWRA-L parameters sufficiently to avoid this artefact. The parameter combinations were therefore filtered by removing any parameter combination that resulted in a significant negative trend in the annual minimal flow between 2019 and 2037. As a result, 6537 parameter sets were removed and the further analysis is based on the remaining 3463 parameter sets.
The goodness of fit between these observed and simulated historical hydrological response variable values is used to constrain the 3463 parameter combinations and select the best 10% of replicates that are used in Section 2.6.1.6 .
2.6.1.5.1.3 Predictions
For each of the 61 model nodes the post-processing of design of experiment results in 3463 time series with a length of 90 years of hydrological response variable values for baseline, ![]() , and coal resource development conditions,
, and coal resource development conditions, ![]() .
.
These two time series are summarised through the maximum raw change, amax, the maximum percent change, pmax, and the year of maximum change, tmax. The percentage change is defined as:
|
|
(1) |
One of the nine hydrological response variables defined in companion submethodology M06 for surface water modelling (Viney, 2016), P01, is not reported in this product. The observed values of P01 in the observation catchments are all zero, which is in accordance with the ephemeral nature of the river system. The changes simulated in this modelling exercise, a climate with less rainfall and coal mine operations that intercept rainfall and potentially increase the loss of surface water to groundwater, can only lead to a decrease in the low flow. As the P01 is already zero, it can decrease no more and it is therefore not necessary to explicitly compute the change in this hydrological response variable.