The OGIA model is calibrated in steady state to replicate long-term mean conditions pre 1995 (i.e. pre CSG extraction) using the PEST suite of software in three steps as described in Section 2.6.2.6 (Parameterisation). Firstly, a preliminary calibration of the steady-state regional model is used to provide initial heads and boundary conditions for the transient sub-model. Secondly, the transient sub-model is calibrated using detailed groundwater level data for the Walloon Coal Measures near the existing Kogan North/Daandine CSG field. Finally, the steady-state regional model is recalibrated using calibrated hydraulic conductivity values for the Walloon Coal Measures from the transient calibration within the sub-model area.
The overall process is referred to as calibration-constrained uncertainty analysis and is also known as Null-space Monte Carlo Analysis (Tonkin and Doherty, 2009). Similar to standard Monte Carlo approaches, 200 stochastic parameter fields are generated using an appropriate covariance matrix of innate parameter variability defined by the modeller. Then for each of these parameter fields, the difference between the random field and the calibrated parameter field are obtained and projected onto the calibration null space. The parameter field arising from the calibration then replaces the solution-space component of the stochastically generated field. Calibration solution space and null space mentioned herein refers respectively to the combination of parameter sets that, respectively, can and cannot be estimated using the calibration dataset. Details of this uncertainty analysis method are documented in WaterMark Numerical Computing (2012). The mathematical implementation of this uncertainty analysis differs from the approach for other bioregional assessments described in companion submethodology M09 (Propagating uncertainty through models) (Peeters et al., 2016). However, the underlying concept of stochastically generating a posterior predictive probability distribution, constrained by relevant observation data is equivalent. The OGIA model uncertainty analysis is able to give probabilistic estimates of the hydrological changes associated with coal resource development and thus meets the BA uncertainty analysis requirements.
The 200 calibration-constrained parameter sets varied net recharge values spatially for 20 recharge zones as described in Section 2.6.2.4 (Boundary and initial conditions). GHD (2012) state ‘modelled net or effective recharge rates … are comparable with the estimates of Kellett et al. (2003)’. Specific storage (Ss) varies spatially in the productive coal layers (Walloon Coal Measures and Bandanna Formation) or is assigned a constant storage value for other confined model layers for which observed groundwater levels were not available. Specific yield is used to define unconfined storage values for the aquifer outcrop areas, Condamine Alluvium, Main Range Volcanics and alluvium outside the Condamine area. Model storage values for each model layer are described in Section 2.6.2.6 (Parameterisation).
The formal uncertainty analysis considered hydraulic conductivity, recharge and storage values, but did not consider model conceptualisation or the parameters used to specify drain and river boundary conditions. However, model predictions are unlikely to be sensitive to the assigned Drain and River cell conductance values as the ‘use of a relatively high value ensures that:
- Modelled groundwater levels do not significantly exceed the modelled ground surface; and
- Modelled discharges are typically controlled by the hydraulic properties of the underlying layers’ (GHD, 2012, p. 58).
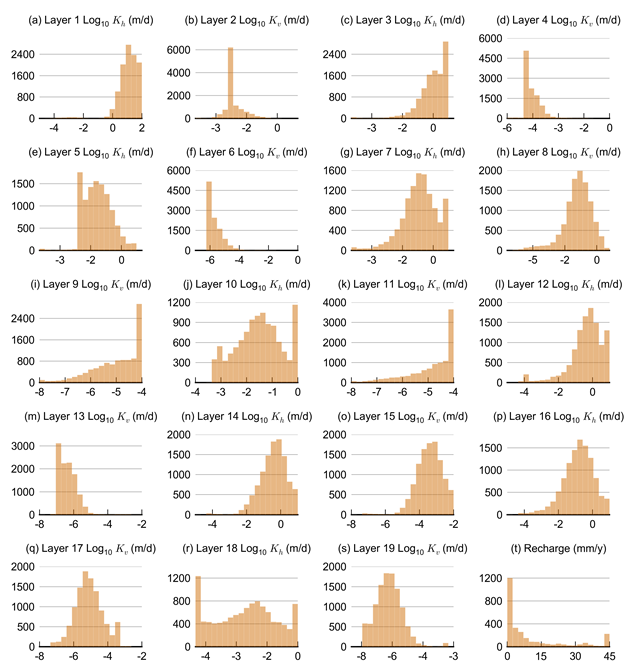
The posterior distributions of hydraulic conductivity (Figure 15) show that the calibration-constrained hydraulic conductivity parameters (Kh and Kv) vary over several orders of magnitude in each layer of the OGIA model. Most parameter values vary by at least one order of magnitude from the median value for that model layer. Modelled recharge values have a skewed distribution, with most values being less than 10 mm/year (Figure 15). Storage values for each model layer are described in Section 2.6.2.6 (Parameterisation).
Model layer names are described in Figure 6 (Section 2.6.2.3). Horizontal hydraulic conductivity (Kh) values are shown for aquifers and vertical hydraulic conductivity (Kv) values are shown for aquitards.
Data: Bioregional Assessment Programme (Dataset 1)
