The conceptual model for the Maranoa-Balonne-Condamine subregion (in companion product 2.3 (Holland et al., 2016)) indicates that coal resource development has the potential to directly affect the regional groundwater and surface water systems. Hydrological changes to the groundwater system can propagate through the alluvium and other aquifers to indirectly affect groundwater-dependent ecosystems and surface water – groundwater interactions in the aquifer outcrop and subcrop areas. Hydrological changes to the surface water system can affect deep soil drainage and surface water – groundwater interactions in aquifer outcrop areas.
Coal resource development in the Maranoa-Balonne-Condamine subregion may have a wide range of water-related impacts. For example, coal mining may affect surface water drainage, potentially affecting surface water quality, direction, flow and volume. Mining can also affect deep soil drainage in aquifer outcrop areas, which can change groundwater quality, aquifer properties, groundwater composition and pressure. Surface water – groundwater interactions in aquifer outcrops can be affected by coal mining and CSG development, potentially affecting groundwater quality, flow (reduction) and level. Coal resource development can also change groundwater conditions (including groundwater quality, aquifer properties, flow (reduction), level and pressure) in affected aquifers. CSG development primarily affects groundwater pressure in the coal seams, potentially leading to subsurface depressurisation of other aquifers and aquitards where direct hydraulic connections exist. Direct hydraulic connections may occur preferentially via geological structures such as faults, or more diffusely where direct stratigraphic contact exists between layers.
As outlined in companion submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016), different model types and model codes are chosen in a bioregional assessment (BA) depending on the specific requirements of each subregion or bioregion. Specifically, the groundwater model needs to deliver spatially explicit model outputs that are used as inputs to other BA models, that can include surface water modelling, uncertainty analysis and receptor impact modelling, and to directly evaluate impact on water resources. Table 3 lists the criteria used to assess whether a groundwater model is considered to be fit for purpose for BA. Beneath the table, the general BA groundwater modelling requirements and the rationale for whether the approach used in the Maranoa-Balonne-Condamine subregion meets the criteria are discussed.
Table 3 Assessment of groundwater numerical modelling approach in the Maranoa-Balonne-Condamine subregion
Prediction of hydrological response variables
The objective of groundwater modelling undertaken as part of a BA is to probabilistically assess hydrological changes arising from coal resource development at water-dependent assets and receptors (see companion submethodology M07 (as listed in Table 1) for groundwater modelling (Crosbie et al., 2016)). Groundwater modelling predicts hydrological response variables, the hydrological characteristics of the system or landscape class that potentially change due to coal resource development. These outputs from the groundwater modelling can be either fluxes or stores. They need to be decided before the sensitivity analysis begins and also need to be defined precisely ‒ for example, drawdown at receptor location (x, y, z) at time t. The hydrological response variables for groundwater are maximum drawdown (dmax) and time to maximum drawdown (tmax).
In order to quantify uncertainties associated with model prediction, groundwater models in BA need to be run probabilistically and not deterministically. Consequently, this means that model predictions are not unique values but probability distributions. Mismatches in scale between the regional nature of the modelling and the point-scale nature of the receptors means that the modelling is not able to capture fine-scale complexities of impacts upon receptors. Receptors that are directly relevant to groundwater modelling in the Maranoa-Balonne-Condamine subregion are point locations associated with groundwater bores (economic bores). The source aquifer (or model layer) of each bore is based on information supplied by the Queensland Office of Groundwater Impact Assessment (OGIA) and used in the assessment of cumulative impacts of coal seam gas (CSG) development in the Surat cumulative management area (CMA). In BA, the focus is on the difference between two possible futures – the baseline and the coal resource development pathway (CRDP). Numerical groundwater modelling results are primarily presented as the difference in groundwater drawdown between the baseline and CRDP futures. This approach reduces uncertainty as there is ‘less uncertainty when a prediction can be formulated as a subtraction of two model results’ (Barnett et al., 2012).
Integration of the groundwater model with a surface water numerical model and receptor impact modelling is not possible at this time in the Maranoa-Balonne-Condamine subregion for two reasons. Firstly, long-term, consistent water quality and water quantity data measurements of surface water and groundwater systems are not available in the Maranoa-Balonne-Condamine subregion (see companion product 1.5 for the Maranoa-Balonne-Condamine subregion (Cassel et al., 2015)). Secondly, the OGIA model (QWC, 2012) is ‘a regional groundwater flow model for making predictions of groundwater impacts from the petroleum and gas activities and for developing the Spring Impact Management Strategy’ (QWC, 2012). As such, its focus is the deep regional aquifers targeted by CSG development, which means that the OGIA model may not on its own be suitable for assessing hydrological changes in surficial aquifers that are important in representing impacts to surface water – groundwater interactions and groundwater-dependent ecosystems. The combination of limited water quality and quantity data availability and use of a model that is focused on the deeper regional aquifer limits the value of developing a coupled surface water – groundwater numerical model in the Maranoa-Balonne-Condamine subregion at this time.
The implications of not developing a coupled surface water – groundwater numerical model are that several companion products are not required or cannot be produced for the BA in the Maranoa-Balonne-Condamine subregion. Companion product 2.1-2.2 (observations analysis, statistical analysis and interpolation) for the Maranoa-Balonne-Condamine subregion is not required because: (i) the Assessment team did not develop a surface water numerical model; and (ii) the development of the OGIA model is well documented (GHD, 2012; QWC, 2012). Companion product 2.5 (water balance assessment) for the Maranoa-Balonne-Condamine subregion, is not produced; instead, the water balance is documented in Section 2.6.2.7. Companion product 2.7 (receptor impact modelling) for the Maranoa-Balonne-Condamine subregion is not produced because the Assessment team cannot use surface water numerical modelling to define the zone of potential hydrological impact or quantify hydrological response variables related to the surface water systems that are necessary for this product. The analysis of surface water – groundwater interactions using a combination of outputs from the numerical groundwater model and the conceptual model of causal pathways that describes the logical chain of events ‒ either planned or unplanned ‒ that link coal resource development and potential impacts on water and water-dependent assets will inform the assessment of indirect impacts in companion product 3-4 (risk and impact analysis).
Design and construction
The Australian groundwater modelling guidelines (Barnett et al., 2012) advise that it is essential to clearly state the design objectives of the groundwater model and the model confidence level. Modelling objectives are stated above. The model confidence level is an a priori categorisation of a groundwater model to reflect its predictive capability as a function of the model complexity, prediction timeframe and data availability. As described in companion submethodology M07 for groundwater modelling (Crosbie et al., 2016), all groundwater models used in BAs, including the OGIA model, are ‘Class 1’ models as defined by the Australian groundwater modelling guidelines (Barnett et al., 2012). This is the lowest level of certainty within the classification and is a reflection of the data available and predictions required, rather than the quality of the models. Key indicators of Class 1 models include that model predictive time frames are more than ten times longer than the length of the transient model calibration period, and that the magnitude of stresses featured in prediction scenarios is more than five times larger than simulated in the calibration period (Barnett et al., 2012).
The major assumptions and model choices related to model development are described in Section 2.6.2.3. The effect of the assumptions and model choices on predictions are discussed in the qualitative uncertainty analysis in Section 2.6.2.8. The level of detail within the conceptual model meets the objectives of Guiding Principle 3.1 and Guiding Principle 3.3, being based on interpretation of available data (Barnett et al., 2012). The groundwater model domain encompasses current and future key stresses related to coal resource development, which meets the modelling guiding principles (Barnett et al., 2012). Model vertical and horizontal discretisation and use of more detailed sub-models (e.g. Condamine Alluvium and transient) represent a compromise between technical and resource requirements for a regional-scale groundwater model, thus meeting the modelling guiding principles (Barnett et al., 2012). The OGIA model uses steady-state calibration to define initial conditions for transient simulations, which meets the modelling guiding principles (Barnett et al., 2012).
The objectives of numerical modelling in BA are not to simulate the state of groundwater under the baseline and coal resource development futures, but to quantify the difference between the two futures. This approach allows a number of simplifying assumptions to be made based on the principle of superposition (Reilly et al., 1987). The principle of superposition means that for linear systems, the solution to a problem involving multiple inputs (or stresses) is equal to the sum of the solutions to a set of simpler individual problems that form the composite problem. To assess the effect of change in a stress, such as depressurisation and dewatering for coal resource development, it is sufficient to only estimate the change in stress. It is not necessary to estimate the initial conditions in the aquifer or other fluxes and stresses, provided these do not change (Barlow and Leake, 2012). The principle of superposition is used for many pump test analyses, where aquifer parameters are inferred from the change in stress (pumping rate) and change in groundwater level (drawdown) (Kruseman and de Ridder, 1994).
The principle of superposition is only valid for linear systems, i.e. systems where the response to a change in stress is proportional to the change in the stress. In other words, where a doubling of stress will result in a doubling of the response. In groundwater flow dynamics this condition is satisfied for confined aquifers. Unconfined aquifers are not strictly linear, as aquifer transmissivity depends on the saturated thickness. Reilly et al. (1987) and Rassam et al. (2004) do show however that the concepts are still valid for mild violations of the linearity conditions.
Surface water and groundwater numerical modelling in BA are run under historical conditions for the 30-year period from 1 January 1983 to 31 December 2012. It is assumed that after 90 years of simulation the coal seam gas (CSG) and large coal mining development that is simulated has ceased operation (Crosbie, et al., 2016). The further into the future that the impacts of large coal mines and coal seam gas developments are simulated, the more uncertainty there is in the estimation of future conditions. These future conditions include the future climate, land use and water sharing rules. In BA, the historical climate time series is repeated three times to create a 90-year time series and modified to be consistent with a median future climate projection as described in companion submethodology M06 (as listed in Table 1) for surface water modelling (Viney, 2016). This 30-year period is repeated to ensure that the effect of droughts and floods does not confound the comparison between time periods. While the same time periods are reported in the Maranoa-Balonne-Condamine subregion, the OGIA model uses long-term mean recharge rates instead of time-varying climate input data. The focus on the difference between two possible futures in BA means that there is no need to assess the effect of climate change assumptions on predictions (e.g. Guiding Principle 6.2 in Barnett et al. (2012)).
Integration with sensitivity and uncertainty analysis workflow
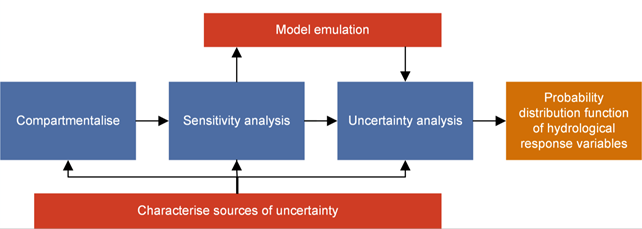
Figure 3 outlines the methodology for propagation of uncertainty within the BA as described in companion submethodology M09 (as listed in Table 1) for propagating uncertainty through models (Peeters et al., 2016). Firstly, the conceptual model is compartmentalised (i.e. subdivided into a number of sub-models without feedback loops) and points of interactions between sub-models are identified. A point of interaction is where the output of one model is input to the linked model. Secondly, a sensitivity analysis is carried out to identify the model factors (parameters and assumptions) that have the largest impact on the hydrological response variables of interest. When carried out for each sub-model, probability distribution functions can be described for each hydrological response variable.
Figure 3 Uncertainty methodology flowchart
Next, quantitative uncertainty analysis numerically evaluates the degree to which each of the model inputs (parameters) affects the model predictions by running the model thousands of times and varying the values of the input parameters through a precisely defined and randomised range of values. However, many model choices and assumptions cannot be evaluated in the quantitative analysis. Instead, the qualitative uncertainty analysis describes the rationale for and scores the effect of each assumption on model predictions. Each assumption is scored on four attributes related to: (i) data availability, (ii) resource availability, (iii) technical and computational limitations and (iv) effect on model predictions. The sensitivity and uncertainty workflow is consistent with the groundwater modelling guiding principles (Barnett et al., 2012).
There is an explicit acknowledgement that not all of the information required to build an ideal groundwater flow model will be available. Therefore, assumptions will need to be made with regards to model conceptualisation and parameterisation. Model assumptions are deemed valid in the context of BA modelling if there is no or minimal effect on predictions, or that it will overestimate hydrological changes. The uncertainties associated with these assumptions are quantified and then propagated from conceptual modelling to receptor impact modelling wherever possible in BAs. The OGIA model uncertainty analysis, while not identical to that used in other BAs, is able to give probabilistic estimates of the hydrological changes associated with coal resource development and thus meets the BA uncertainty analysis requirements (see companion submethodology M09 (as listed in Table 1) for propagating uncertainty through models (Peeters et al., 2016)).
The sensitivity and uncertainty analyses undertaken for BAs require that groundwater models are robust, that is, capable of converging for a broad range of parameter values. Parameter values are changed in an automated way to enable thousands of model runs using plausible parameter values and extreme parameter combinations for model stress testing. The OGIA sensitivity and uncertainty analysis, that is, 200 calibration-constrained parameter sets, where spatial parameters are defined using pilot points, is consistent with the BA sensitivity and uncertainty analysis requirements. Each parameter set consists of 3300 parameters. Like most inverse-problems, calibration of this highly parameterised groundwater model is an ill-posed problem. However, Null-Space Monte Carlo analysis, as used in this study, provides an efficient method to explore the non-uniqueness of model parameters and resulting model prediction uncertainty. The pilot points give spatial coherence to the model parameter values that is consistent with the model conceptualisation and use regularisation to solve the problem mathematically.
Water balance components
The water balance is reported for a defined control volume in BA that includes all hydrologically connected changes that are potentially predicted by the surface water and groundwater models. The water balance components (e.g. recharge, evapotranspiration, baseflow (discharge to stream), licensed extractions, upward flow from deeper groundwater and change in storage) are compared with estimates of fluxes described in the regional-scale conceptual model and localised groundwater models to provide confidence in model predictions, thus meeting the modelling guiding principles (Barnett et al., 2012). Section 2.6.2.7 compares model estimates of water extraction from CSG and open-cut coal mining with available local and regional estimates.
Estimates of diffuse recharge for BA groundwater models are typically obtained from the Australian Water Resource Assessment (AWRA) models as described in companion submethodology M06 (as listed in Table 1) for surface water modelling (Viney, 2016). In the OGIA model, net recharge values are parameterised spatially using pilot points to define the calibration-constrained parameter sets. Rates of groundwater extraction for stock, domestic, irrigation, industry and town water supplies are modelled as constant and equal to the rates applicable to the last quarter of 2012 (unless actual metered data are available) in BA. The OGIA model estimates extraction volumes using information contained in the relevant water resource plans using a constant rate starting in 1995 in the Base Run that accounts for all non petroleum and gas water extraction. Groundwater extraction associated with CSG and large coal mining development is generally determined based on target groundwater levels rather than extraction rates in BA, which means that groundwater extraction is a function of the hydraulic properties of the aquifers and aquitards involved (which are uncertain) and will be estimated as a probability distribution rather than as a discrete value. This is consistent with using the MODFLOW EVT package to simulate CSG extraction and the Drain package to represent mine pit dewatering in the OGIA model.
Evapotranspiration for areas with shallow watertables is typically represented using a depth-dependent boundary condition in BA groundwater models. This permits hydrological response variables related to terrestrial groundwater-dependent ecosystems to be incorporated into the groundwater models. This assumption is not met by the OGIA model, as it is focused on the deeper regional aquifers targeted by CSG development.
Surface water – groundwater interactions are generally modelled in BA using variously coupled landscape, river and groundwater models. Coupled landscape, river and groundwater models pass river stages, exchange fluxes and coal development fluxes (e.g. co-produced water discharged to streams) between models to estimate hydrological response variables for receptor impact modelling. Subregions that do not have coupled river and groundwater models have limited surface water – groundwater interaction modelling and cannot estimate river stages at receptor locations. This is the case for the Maranoa-Balonne-Condamine subregion. The MODFLOW River and Drain packages are used to represent surface water – groundwater interactions in the OGIA model, which assumes that all surface watercourses act as groundwater discharge boundaries. This is ‘considered to be a conservative assumption from an impact point of view’ and ‘effectively assumes that all surface watercourses act as discharge boundaries and hence cannot leak’ (GHD, 2012).
The OGIA model is able to probabilistically estimate the hydrological response variables for groundwater, that is, maximum drawdown (dmax) and time to maximum drawdown (tmax) and is used to identify water bores and springs potentially affected by drawdown caused by petroleum and gas extraction in the Surat cumulative management area (QWC, 2012). However, the focus on the deep regional aquifers targeted by CSG development, means that integration of the groundwater model with a surface water numerical model and receptor impact modelling is not possible at this time in the Maranoa-Balonne-Condamine subregion. Assumptions related to the representation of water balance components in the OGIA model are described in Section 2.6.2.4, Section 2.6.2.7 and discussed in Section 2.6.2.8.
Transparent and reproducible model outputs
An over-arching requirement of the BAs is for all model outputs to be transparent and reproducible, which means that the models need to be run as part of a documented workflow that records the provenance of the input data, executables and outputs. This is achieved through the use of scripting in BAs. All pre-processing, model runs and post-processing is done using scripts that are made available along with the products; this ensures that all model inputs, parameters, executables and outputs are traceable, meeting the modelling guiding principles related to transparency (Barnett et al., 2012).
The OGIA model is a proprietary model owned and operated by OGIA. For this reason, the model itself cannot be made publicly available by the Bioregional Assessment Programme. Instead, the Assessment team and OGIA have agreed to make the relevant BA groundwater model inputs and outputs publicly available (Australian Government, 2016).
Product Finalisation date
- 2.6.2.1 Methods
- 2.6.2.2 Review of existing models
- 2.6.2.3 Model development
- 2.6.2.4 Boundary and initial conditions
- 2.6.2.5 Implementation of coal resource development pathway
- 2.6.2.6 Parameterisation
- 2.6.2.7 Observations and predictions
- 2.6.2.8 Uncertainty analysis
- 2.6.2.9 Limitations
- Glossary
- Citation
- Acknowledgements
- Contributors to the Technical Programme
- About this technical product