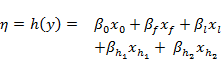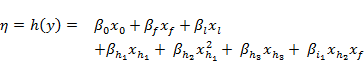2.7.3.3.1 Qualitative mathematical models
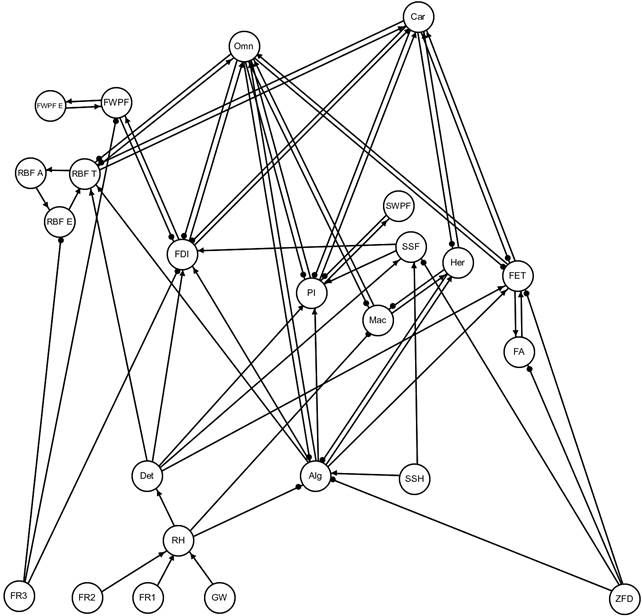
Workshop discussions on intermittent stream reaches determined that, while flowing, they could be adequately described by a modified version of the signed digraph for perennial streams (Figure 16). The model for this system lacks pool-breeding frog species, a group which is instead replaced with non-specialist breeding frogs, but otherwise is identical in its basic model components and linkages. This model also lacks the influence of the regime for perennial flow over riffle substrate as a main driver for success of riffle-breeding frog eggs, flow-dependent macroinvertebrates and fishes preferring fast-water habitats.
Figure 16 Signed digraph of intermittent stream communities of the Hunter Valley
Algae (Alg), carnivores (Car), detritus (Det), frog adults (FA), frog eggs and tadpoles (FET), eggs of fast water preferred fishes (FWPF E), fast water preferred fishes (adults) (FWPF), herbivores (Her), flow-dependent invertebrates (FDI), macrophytes (Mac), omnivores (Omn), pool invertebrates (PI), adults of riffle-breeding frogs (RBF A), eggs of riffle-breeding frogs (RBF E), tadpoles of riffle-breeding frogs (RBF T), riparian habitat (RH), subsurface habitat (SSH), subsurface fauna (SSF), slow water preferred fishes (SWPF). Hydrological variables added subsequent to the qualitative modelling workshop are flow regimes 1, 2 and 3 (FR1, FR2, FR3), depth to groundwater (GW) and zero-flow days (ZFD).
Data: Bioregional Assessment Programme (Dataset 1)
Surface water and groundwater modelling indicated significant potential impacts of coal mining to surface flow and groundwater for this landscape class. The impacts for this system are the same as for perennial streams, and include the same hydrological response variables of overbench flow (flow regime 1, FR1), overbank flow (flow regime 2, FR2), low flows (flow regime 3, FR3), zero-flow days (ZFD), and depth to groundwater (GW). As in the perennial streams model, water quality variables are not represented, although water quality is acknowledged as an important component of instream habitat.
In this system, a diminishment in FR1 and FR2 was treated as having a negative effect on riparian habitat (RH in Figure 16), while a decrease in FR3 was treated as having a negative effect on flow-dependent invertebrates (FDI), riffle-breeding frogs (RBF) and fast water preferred fishes (FWPF). An increase in the number of zero-flow days was described as having a negative effect on (non-specialist) frog eggs and tadpoles (FET), subsurface fauna (SSF), flow-dependent invertebrates (FDI), the quality of subsurface habitat (SSH) and algae (Alg). Finally, a decrease in groundwater levels was described as having a negative impact on riparian habitat and subsurface habitat. Based on all possible combinations of these impacts (again with FR1 and FR2 considered in unison), a total of 15 cumulative impact scenarios were developed for qualitative analyses of response predictions (Table 14). In practical terms, the structure of this model and the pathways of interaction effects of the hydrological response variables give a system that has equivalent response predictions to that of model 2 for perennial streams (Figure 13, Table 8).
Table 14 Summary of the cumulative impact scenarios (CISs) for intermittent streams for the Hunter subregion
Pressure scenarios are determined by combinations of no-change (0), increase (+) or decrease (-) in the following hydrologic response variables: flow regime 1 (FR1, overbench and bank-full flow), flow regime 2 (FR2, overbank flow), flow regime 3 (FR3, low flow), zero-flow days (ZFD), depth to groundwater (GW).
Data: Bioregional Assessment Programme (Dataset 1)
Qualitative analysis of this signed digraph model confirms that the intermittent stream system (Figure 16, Table 15) has exactly the same qualitative response predictions as model 2 for perennial streams (Figure 13, Table 8). Most response predictions are negative, if not ambiguous, with only macrophytes and herbivores having positive response predictions across the 15 scenarios. As before, riffle-breeding frogs are predicted to increase in some scenarios in part due to release from predation.
Table 15 Predicted response of the signed digraph variables in intermittent streams to (cumulative) changes in hydrological responses variables
The cumulative impact scenarios (C1 to C15) are determined by combinations of no-change (0), increase (+) or decrease (-) in hydrologic response variables (see Table 14). Qualitative model predictions show the predicted response of the signed digraph variable. Predictions that are completely determined are shown without parentheses. Predictions that are ambiguous but with a high probability (0.80 or greater) of sign determinacy are shown with parentheses. Predictions with a low probability (less than 0.80) of sign determinacy are denoted by a question mark. Zero denotes completely determined predictions of no change.
Data: Bioregional Assessment Programme (Dataset 1)
2.7.3.3.2 Temporal scope, hydrological response variable and receptor impact variables
The temporal scope for the intermittent streams is the same as that described for the perennial streams. For surface water and groundwater variables the reference assessment interval is defined as the 30 years preceding 2012 (i.e. 1983 to 2012). For surface water variables, the short-assessment interval is defined as the 30 years preceding the short-assessment year (i.e. 2013 to 2042), and similarly the long-assessment interval is defined as the 30 years that precede the long-assessment year (i.e. 2073 to 2102). For groundwater, maximum drawdown (metres) and time to maximum drawdown are considered across the full 90-year window (i.e. 2013 to 2102).
Following advice from participants during (and after) the qualitative modelling workshop, and guided by the availability of experts for the receptor impact modelling workshop, and the receptor impact variable selection criteria, the receptor impact models were originally designed to focus on the relationship between subsurface habitat and zero-flow days, and riffle-breeding frogs and low flow. However, due to the reservations surrounding the definition of ‘low flow’, and its sensitivity to stream channel geometry (which varies across the landscape class), the experts at the receptor impact modelling workshops again elected to change the low-flow hydrological response variable to zero-flow days (Table 16).
At the receptor impact modelling workshop, hyporheic invertebrate taxa richness was selected by the experts as a suitable indicator of subsurface habitat quality, hence the receptor impact model for intermittent streams focused on the following relationships:
- Mean richness of hyporheic invertebrate taxa in 6 L of water pumped from a depth of 40 cm below the streambed (riffle and gravel bars; Hancock, 2004), to changes in ZQD (subsequently referred to in this Section as ‘zero-flow days) and ZME
- Mean probability of presence of the riffle-breeding frog (Mixophyes balbus) in a 100-m transect, to changes in ZQD and ZME.
Table 16 Summary of the hydrological response variables used in the receptor impact models, together with the signed digraph variables that they correspond to, for intermittent streams in the Hunter subregion
2.7.3.3.3 Receptor impact models
2.7.3.3.3.1 Hyporheic invertebrate taxa richness
The richness of hyporheic invertebrate taxa has been proposed as an indicator of health in intermittent rivers, similarly to macroinvertebrate richness in permanent rivers (Leigh et al., 2013). The advantage of the hyporheic zone for monitoring the condition of temporary rivers is that hyporheic invertebrates within temporary rivers can be sampled from beneath both dry and wet channels, and across multiple seasons. Aquatic invertebrates often persist beneath surface channels in moist or dry sediments, even during long dry phases, and are sensitive to groundwater quality (Malard et al., 1996).
Elicitation scenarios
Table 17 summarises the elicitation matrix for the mean richness of hyporheic invertebrate taxa. The first six design points – design point identifiers 1 to 6 – address the predicted variability in ZQD and ZME across the landscape class in the reference interval, capturing the lowest and highest predicted values together with one intermediate value. These design points provide for an estimate of the uncertainty in mean hyporheic invertebrate taxa richness across the landscape class in the reference year 2012 (Yref).
Design points 8 to 19 represent scenarios that span the uncertainty in the predicted values of ZQD and ZME in the relevant time period of hydrological history associated with the short (2042) and long (2102) assessment years, combined with high and low values of Yref. The high and low values for Yref were again calculated during the receptor impact modelling workshop.
Table 17 Elicitation design matrix for the receptor impact model of mean hyporheic invertebrate taxa richness in intermittent streams for the Hunter subregion
Design points for Yref in the future (short- and long-assessment periods) are calculated during the receptor impact modelling elicitation workshop using elicited values for the receptor impact variable in the reference period. All other design points (with identifiers) are either default values or values determined by groundwater and surface water modelling. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, na = applicable
Data: Bioregional Assessment Programme (Dataset 1)
Receptor impact model
The fitted model for mean hyporheic invertebrate taxa richness takes the form
|
|
(3) |
here the terms ![]() are as before and
are as before and ![]() is the integer value of ZQD and
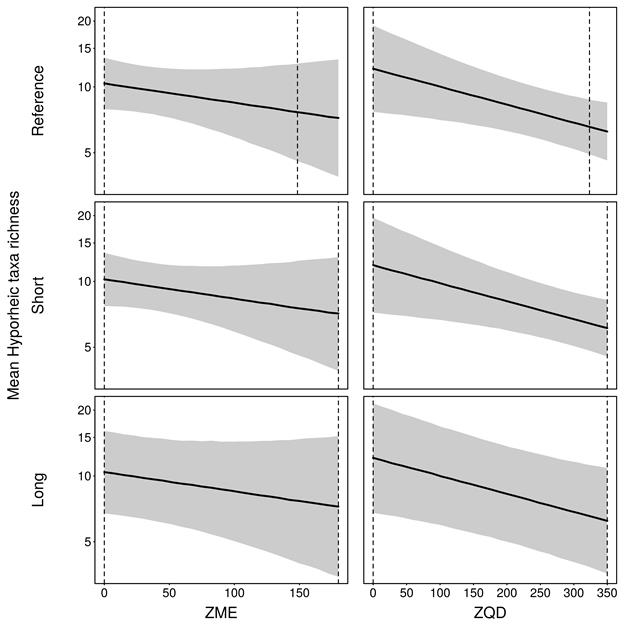
is the integer value of ZQD and ![]() is the integer value of ZME. The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 17, whilst Table 18 summarises the same information for all five model coefficients.
is the integer value of ZME. The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 17, whilst Table 18 summarises the same information for all five model coefficients.
The model indicates that the experts’ elicited information strongly supports the assertion that ZQD and ZME have a negative effect on the mean richness of hyporheic invertebrate taxa despite the experts being quite uncertain about its average value. The model suggests that it can vary substantially across the landscape class from <10 to almost 20 per sampling unit under conditions of constant flow (ZQD = 0), holding all other covariates at their mid-values. As the number of zero-flow days increase, however, experts were of the opinion that density would drop to values from 5 to 8 under very intermittent flow conditions (ZQD > 320 days) (Figure 17).
There was very little evidence in the elicited data to suggest that this effect would be substantially different in the future-assessment years. Again, this is indicated by the almost-identical partial regression plots in the reference-, short- and long-assessment years (Figure 17), and the relatively symmetric negative 10th and positive 90th percentiles for the long and future coefficients in Table 18. The model does, however, suggest that the experts’ uncertainty increased slightly for predictions in the future-assessment years relative to the reference year.
The best-fitting model in this case has also eliminated the possibility that the mean richness of hyporheic invertebrate taxa in the reference years has an influence on its density in the future years. This is indicated by the fact that the coefficient ![]() has not been included in the best-fitting model (Table 18). This suggestion is consistent with the assertion that there is likely to be very little lag in the response of short-lived species to changes in the hydrological response variables.
has not been included in the best-fitting model (Table 18). This suggestion is consistent with the assertion that there is likely to be very little lag in the response of short-lived species to changes in the hydrological response variables.
In middle and bottom rows, all other hydrological response variables are held constant at the midpoint of their elicitation range (during risk estimation all hydrological response variables vary simultaneously). Dashed vertical lines show range of hydrological response variables used in the elicitation. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
Table 18 Mean, 10th and 90th percentile of the coefficients of the receptor impact model for mean hyporheic invertebrate taxa richness in intermittent streams for the Hunter subregion
|
|
Mean |
q10 |
q90 |
|---|---|---|---|
|
(Intercept) |
2.64 |
2.29 |
3 |
|
future1 |
0.0112 |
–0.33 |
0.352 |
|
long1 |
0.0193 |
–0.496 |
0.534 |
|
ZME |
–0.00203 |
–0.0058 |
0.00174 |
|
ZQD |
–0.00189 |
–0.00335 |
–0.000431 |
Future is a binary variable scored 1 if the analysis case is in a short- or long-assessment year. Long is a binary variable scored 1 if the analysis case is in the long assessment year. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
2.7.3.3.3.2 Presence of riffle-breeding frogs
The density and diversity of frogs in streams responds to local, ground-level stream and vegetation variables (Parris and McCarthy, 1999). Many frogs that breed in permanent water bodies are excluded from temporary ones because their larval stage is longer than the persistence of water in these habitats. Therefore, the mix of frog species found in different streams can be partially explained by the different periods of water availability needed by each species in order to breed successfully (Brisbane City Council, 2010).
Elicitation scenarios
Table 19 summarises the elicitation matrix for the presence of the riffle-breeding frog in the intermittent streams of the Hunter subregion. The first six design points – design point identifiers 1 to 6 – address the predicted variability (across the intermittent streams in the landscape class during the reference interval) in ZQD and ZME. The design points 6, 1 and 2 capture the combination of the extremes of each hydrological response variable, whilst design points 3, 5 and 4 represent intermediate points in each hydrological response variable axis.
The remaining design points represent hydrological scenarios that span the uncertainty in the values of the hydrological response variables in the relevant time period of hydrological history associated with the short (2042) and long (2102) assessment years. The high and low values for Yref were again calculated during the receptor impact modelling workshop.
Table 19 Elicitation design matrix for the receptor impact model of the mean probability of presence of the riffle-breeding frog in intermittent streams for the Hunter subregion
Design points for Yref in the future (short- and long-assessment periods) are calculated during the receptor impact modelling elicitation workshop using elicited values for the receptor impact variable in the reference period. All other design points (with identifiers) are either default values or values determined by groundwater and surface water modelling. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, na = not applicable
Data: Bioregional Assessment Programme (Dataset 1)
Receptor impact model
The fitted model for the probability of presence of the riffle-breeding frog takes the form
|
|
(4) |
where the terms ![]() are as before,
are as before, ![]() is the integer value of ZQD,
is the integer value of ZQD, ![]() is the integer value of ZME and
is the integer value of ZME and ![]() Identifies the coefficient for the quadratic term
Identifies the coefficient for the quadratic term ![]() The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 18, whilst Table 20 summarises the same information for all seven model coefficients.
The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 18, whilst Table 20 summarises the same information for all seven model coefficients.
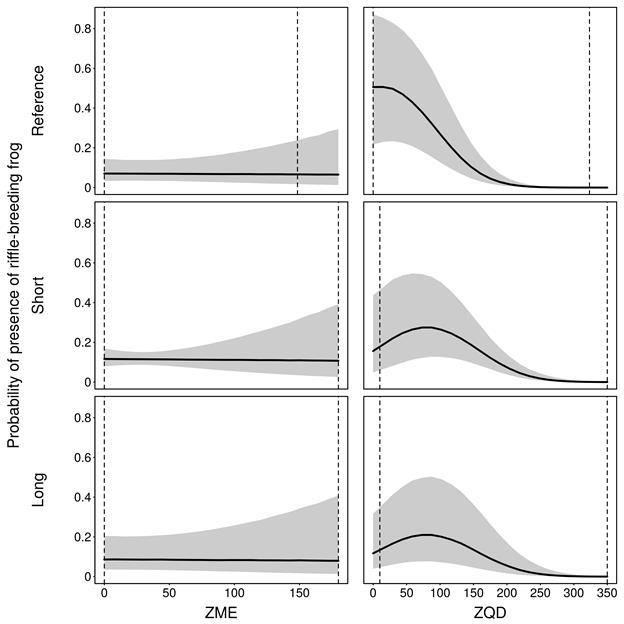
As per the perennial streams model, the hydrological response variable in the intermittent streams model varies during the reference interval and the future interval. The model indicates that the experts’ elicited information strongly supports the assertion that ZQD has a negative effect on the probability of presence of the riffle-breeding frog. The model suggests that the probability of presence can vary across the landscape class from less than 0.2 to 0.8 under conditions of constant flow (ZQD = 0), holding all other covariates at their mid-values. As the number of zero-flow days increase, however, experts were of the opinion that the probability of presence would drop quite dramatically, with the model suggesting some chance of probability of presence of near zero under very intermittent flow conditions (ZQD > 350 days) (Figure 18).
There is evidence in the elicited data that the influence of ZQD on the probability of presence of riffle-breeding frogs may be different in the future assessment years. This is indicated by the positive coefficient of the interaction term ![]() (future1: ZQD, Table 20) and difference in the partial regression plots between the reference year (top) and future years (middle and bottom) (Figure 18).
(future1: ZQD, Table 20) and difference in the partial regression plots between the reference year (top) and future years (middle and bottom) (Figure 18).
The increase in the probability of presence of frogs when zero-flow days are less than 100 appears to be due to the influence of the (highly) uncertain probability of presence when zero flow days are less than 160. The experts’ responses to the elicitation scenarios appears to indicate that when zero flow days are less than 160, other habitat factors are important in determining the probability of frog presence, hence the value of Yref has a strong influence on the expert’s response to the elicitation. As the number of zero flow days increases beyond 160, however, the experts were strongly of the opinion that the increasingly dry conditions will over-ride all other factors and the probability of frogs being present will drop rapidly irrespective of the value of Yref. The automatic model selection procedure included a quadratic coefficient for zero flow days (Table 20) in response to the experts’ elicitations which together with the other variables leads to an increase in frogs at relatively wet conditions due to the value of Yref in the elicitation scenarios (19).
A similar effects occurs in the Perennial streams model (Section 2.7.3.2.3.1) reflected there by a quadratic coefficient for zero flow days but also a positive coefficient for Yref in the best selected model (Table 11). In the intermittent streams model the absence of a Yref coefficient in the best fitted model may be an artefact of the automatic model selection procedure and could be due to a very small difference in the likelihood of the alternative model structure.
The second hydrological variable (ZME) also has a negative effect on the probability of presence of riffle-breeding frogs, although this effect appears to be ecologically less important than the effect of ZQD, as indicated by the near-horizontal partial regression plots.
The best-fitting model in this case suggests that the remaining parameters (intercept and long1) have a limited influence on the probability of presence of the riffle-breeding frog (confidence interval spanning zero, Table 20).
In middle and bottom rows, all other hydrological response variables are held constant at the midpoint of their elicitation range (during risk estimation all hydrological response variables vary simultaneously). Dashed vertical lines show range of hydrological response variables used in the elicitation. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
Table 20 Mean, 10th and 90th percentile of the coefficients of the receptor impact model for probability of presence of the riffle-breeding frog in intermittent streams for the Hunter subregion
Future is a binary variable scored 1 if the analysis case is in a short- or long-assessment year. Long is a binary variable scored 1 if the analysis case is in the long assessment year. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, I(ZQD^2) = zero-flow days quadratic term, future1:ZQD = linear interaction between future 1 and zero-flow days
Data: Bioregional Assessment Programme (Dataset 1)
Product Finalisation date
- 2.7.1 Methods
- 2.7.2 Prioritising landscape classes for receptor impact modelling
- 2.7.3 'Riverine' landscape group
- 2.7.4 'Groundwater-dependent ecosystem' landscape group
- 2.7.5 'Coastal lakes and estuaries' landscape group
- 2.7.6 Limitations and gaps
- Citation
- Acknowledgements
- Contributors to the Technical Programme
- About this technical product