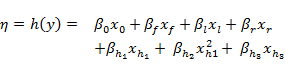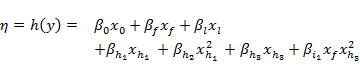2.7.3.2.1 Qualitative mathematical model
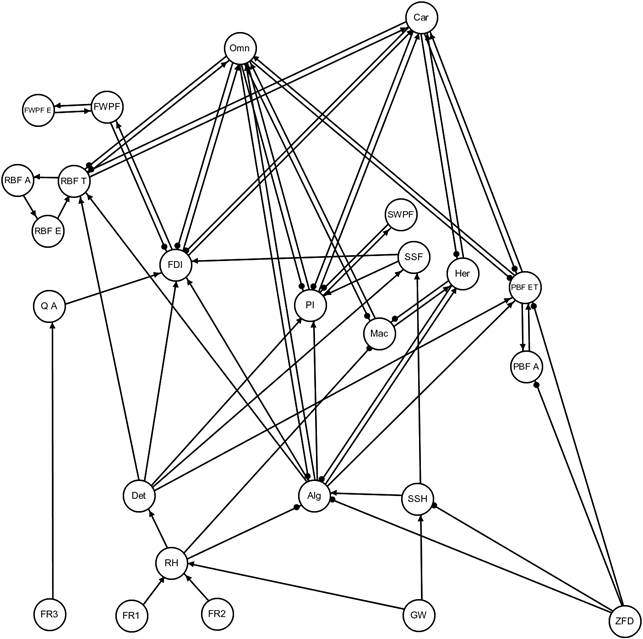
A model for perennial stream reaches was developed based on the stream velocity and habitat preferences of aquatic macroinvertebrates (Figure 12). The model is applicable to other stream biota with a preference for slow or fast flowing water, such as frogs and fish as described below. Water quality variables were purposely not represented in the model, although water quality is acknowledged as an important component of instream habitat. Riparian habitat (RH in Figure 12) in this model primarily pertains to the ‘Forested wetland’ landscape class in the Hunter subregion, for which a separate qualitative model was developed (Section 2.7.4.2). Thus, riparian habitat represents a linking node between the perennial streams and forested wetlands qualitative models. The vegetative canopy of riparian habitat contributes to allochthonous (i.e. found in a different place from its source) stores of detritus (Det) and, through the effect of shade, suppresses the growth of stream macrophytes (Mac) and algae (Alg). Allochthonous inputs of organic matter, in turn drive production of various macroinvertebrate populations (Boulton et al., 2014). Overbench and overbank flows in perennial streams are ecologically important for riparian habitat.
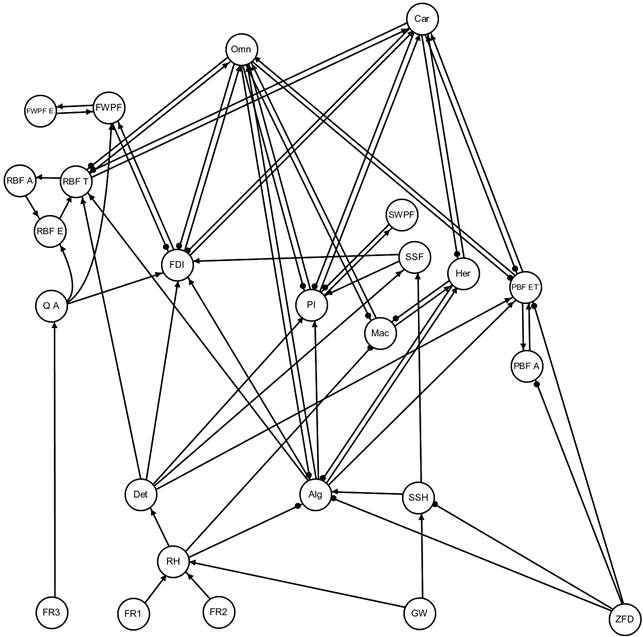
Stream macroinvertebrates were classified into groups based on their affinity for different aspects of stream velocity and flow (i.e. macroinvertebrates which occupy pool habitats and macroinvertebrates associated with fast-water habitats). Flow-dependent invertebrates (LFI and HFI) generally use the upper and interstitial surfaces of riffle substrates, and are considered to be sensitive to changes in the volume and velocity of water flowing over and through riffles (Chessman et al., 2012; Boulton, 2003); hence, flow over riffle substrate was described as a key driver of the productivity of high-flow macroinvertebrates (Q A in Figure 12). There was uncertainty as to whether this is also a strong driver for the success of the egg life stage of riffle-breeding frogs (RBF E) and fishes that prefer fast-water habitats (FWPF E), which led to the development of two alternative signed digraph models that do not (model 1, Figure 12) and do (model 2, Figure 13) include the effect of this driver to frogs and fishes. The effect of zero-flow days (ZFD) on flow-dependent invertebrates is represented via indirect pathways as a result of reduced subsurface habitat, subsurface fauna and algae.
Where present, gravel bars (GB) within the wetted stream channel play a critical role by providing subsurface habitat (SSH) for subsurface fauna and through the filtration of sediment and nutrient cycling, which provides nutrients for primary production (i.e. algae). A group for pool invertebrates (PI) was described for those invertebrates occupying pool habitats. Subsurface fauna (SSF; hyporheos) were defined as those within pool or riffle sediments from 10 cm to 2.5 m depth. The hyporheos feeds mainly on biofilms and includes many types of crustaceans, segmented worms, flatworms, rotifers, water mites, and juvenile stages of aquatic insects (Boulton et al., 1998). The chemical composition of downwelling water travelling through the hyporheic zone is altered by biogeochemical processes mediated by microbial biofilms on sediment particles. The chemically transformed upwelling water can promote growth of periphyton at the streambed surface, creating localised ‘hotspots’ of productivity (Boulton, 2007).
Amphibians and fish were also divided into those preferring riffle or slow-water habitats. An example of a riffle-breeding frog (RBF) is the stuttering frog (Mixophyes balbus), which breeds in streams during summer after heavy rain. Its eggs are laid on rock shelves or shallow riffles in small, flowing streams. The tadpoles are free-swimming benthic grazers, foraging amongst stones and leaf litter in riffle and pool sections of the stream channel (Anstis, 2002). As the tadpoles grow they move to deep, permanent pools and take approximately 12 months to metamorphose. In contrast, the giant burrowing frog (Heleioporus australiacus) is a pool-breeding frog (PBF) that lays its eggs in burrows or under vegetation in small pools. After rains, tadpoles are washed into larger pools where they complete their development in ponded areas.
The climbing galaxias (Galaxias brevipinnis) is an example of a fish that prefers fast water (FWPF) in the headwaters of streams flowing through forested land. This species eats a range of invertebrates including aquatic insects such as mayfly and caddisfly larvae, terrestrial invertebrates such as millipedes, flies and beetles, and crustaceans such as amphipods (Australian Museum, 2013). By contrast, the Australian smelt (Retropinna semoni) is usually found in slow-flowing streams (SWPF) where it schools near the surface. Eggs are laid amongst aquatic vegetation and breeding activity is concentrated into the months preceding summer storms and high, variable stream discharges (Milton and Arthington, 1985). A group of herbivores (Her) was included that consume stream macrophytes and algae. The model includes a group of generalist carnivores (Car) that prey on all of the macroinvertebrate groups and frog tadpoles (RBF T and PBF ET). Top predators in the system, carnivores and omnivores (Omn), generally consume all groups of macroinvertebrates and tadpoles, with omnivores also consuming macrophytes and algae.
Figure 12 Model 1 signed digraph of perennial stream communities of the Hunter Valley
Algae (Alg), carnivores (Car), detritus (Det), eggs of fast water preferred fishes (FWPF E), fast water preferred fishes (adults) (FWPF), herbivores (Her), flow-dependent invertebrates (FDI), macrophytes (Mac), omnivores (Omn), adults of pool-breeding frogs (PBF A), eggs and tadpoles of pool-breeding frogs (PBF ET), pool invertebrates (PI), flow above riffle substrate (Q A), adults of riffle-breeding frogs (RBF A), eggs of riffle-breeding frogs (RBF E), tadpoles of riffle-breeding frogs (RBF T), riparian habitat (RH), subsurface fauna (SSF), subsurface habitat (SSH), slow water preferred fishes (SWPF). Hydrological variables added subsequent to the qualitative modelling workshop are flow regimes 1, 2 and 3 (FR1, FR2, FR3), depth to groundwater (GW) and zero-flow days (ZFD).
Data: Bioregional Assessment Programme (Dataset 1)
Figure 13 Model 2 signed digraph of perennial stream communities of the Hunter Valley
Algae (Alg), carnivores (Car), detritus (Det), eggs of fast water preferred fishes (FWPF E), fast water preferred fishes (adults) (FWPF), herbivores (Her), flow-dependent invertebrates (FDI), macrophytes (Mac), omnivores (Omn), adults of pool-breeding frogs (PBF A), eggs and tadpoles of pool-breeding frogs (PBF ET), pool invertebrates (PI), flow above riffle substrate (Q A), adults of riffle-breeding frogs (RBF A), eggs of riffle-breeding frogs (RBF E), tadpoles of riffle-breeding frogs (RBF T), riparian habitat (RH), subsurface fauna (SSF), subsurface habitat (SSH), slow water preferred fishes (SWPF). Hydrological variables added subsequent to the qualitative modelling workshop are flow regimes 1, 2 and 3 (FR1, FR2, FR3), depth to groundwater (GW) and zero-flow days (ZFD).
Data: Bioregional Assessment Programme (Dataset 1)
Apart from the volume of flow that connects pools by maintaining over-riffle flow, the other hydrological variables that maintain and support the perennial streams ecosystem were identified subsequent to the qualitative modelling workshop. Based on experience gained during the Gloucester subregion assessment, and comments received by experts following the Hunter subregion qualitative modelling workshop, depth to groundwater (GW), frequency, timing and duration of overbench flow (flow regime 1, FR1) and overbank flow (flow regime 2, FR2) were identified as the critical hydrological determinants of riparian habitat condition. Zero-flow days (ZFD in Figure 12 and Figure 13) was also subsequently identified as the most important hydrological determinant of pool-breeding frogs and subsurface habitat.
Over-riffle flow proved more difficult to define, given it varies with channel and substrate morphology, but was broadly agreed to refer to flow above some ‘low-flow’ volume (flow regime 3, FR3). To remove the ambiguity in this term, this volume was identified as the inflection point in a flow-duration curve that indicates a rapid transition from a flowing state to a non-flowing state. By way of example, the flow-duration curve calculated from the Coggan gauging station at the Goulburn River suggests that this flow is 0.03 to 0.06 cm3/s (~2.6–5 ML/day). It was noted, however, that further analysis of flow-duration curves from perennial and intermittent streams in the Hunter subregion would be required to provide further confidence in this definition of ‘low flow’.
In the qualitative models for this landscape class, a diminishment in FR1 and FR2 were both projected to have a negative effect on riparian habitat (RH), while a decrease in FR3 was treated as reducing the flow level above riffle substrates (Q A). An increase in the number of zero-flow days was described as having a negative effect on pool-breeding frogs (PBF), subsurface fauna (SSF), flow-dependent invertebrates (FDI), the quality of subsurface habitat (SSH) and algae (Alg). Finally, a decrease in groundwater level (i.e. an increase in depth to groundwater, GW), was described as having a negative impact on riparian habitat and subsurface habitat. For this landscape class, it was determined that impacts to FR1 and FR2 could not be distinguished in perturbation analyses, and so their effect on the ecosystem could be considered together. Based on all possible combinations of these impacts, with FR1 and FR2 considered in unison, a total of 15 cumulative impact scenarios were developed for qualitative analyses of response predictions (Table 6).
Table 6 Summary of the cumulative impact scenarios (CISs) for perennial streams for the Hunter subregion
Data: Bioregional Assessment Programme (Dataset 1)
Qualitative analysis of the signed digraph models (Figure 12 and Figure 13) generally indicate a negative response prediction for variables within the riparian-dependent community of perennial streams across the 15 cumulative impact scenarios (Table 7 and Table 8). Exceptions include the predicted positive response of macrophytes (Mac) and herbivores (Her), which is primarily a consequence of decreased suppression of macrophytes by riparian habitat. The predicted response of both pool-breeding and riffle-breeding frogs appeared to have a high degree of ambiguity across many of the cumulative impact scenarios, but in a number of scenarios they were predicted to have an increase in density, which was due, in part, to a release from predation as a consequence of a predicted decrease in their omnivore and carnivore predators.
Table 7 Predicted response of the signed digraph variables (model 1) in perennial streams to (cumulative) changes in hydrological response variables
The cumulative impact scenarios (C1 to C15) are determined by combinations of no-change (0), increase (+) or decrease (–) in hydrologic response variables (see Table 6). Qualitative model predictions show the predicted response of the signed digraph variable. Predictions that are completely determined are shown without parentheses. Predictions that are ambiguous but with a high probability (0.80 or greater) of sign determinancy are shown with parentheses. Predictions with a low probability (less than 0.80) of sign determinancy are denoted by a question mark. Zero denotes completely determined predictions of no change.
Data: Bioregional Assessment Programme (Dataset 1)
Table 8 Predicted response of the signed digraph variables (model 2) in perennial streams to (cumulative) changes in hydrological response variables
The cumulative impact scenarios (C1 to C15) are determined by combinations of no-change (0), increase (+) or decrease (–) in hydrologic response variables (see Table 6). Qualitative model predictions show the predicted response of the signed digraph variable. Predictions that are completely determined are shown without parentheses. Predictions that are ambiguous but with a high probability (0.80 or greater) of sign determinancy are shown with parentheses. Predictions with a low probability (less than 0.80) of sign determinancy are denoted by a question mark. Zero denotes completely determined predictions of no change.
Data: Bioregional Assessment Programme (Dataset 1)
2.7.3.2.2 Temporal scope, hydrological response variables and receptor impact variables
In bioregional assessments (BAs), the potential ecological impacts of coal resource development are assessed in two future years: 2042 and 2102. These are labelled as the short- and long-assessment years, respectively. Potential ecological changes are quantified in BAs by predicting the state of a select number of receptor impact variables in the short- and long-assessment years. These predictions are made conditional on the values of certain groundwater and surface water statistics that summarise the numerical model predictions in a defined assessment interval that precedes the assessment year. In all cases these predictions allow for the possibility that the future result can depend on the state of the receptor impact variable in the reference year 2012, and consequently this is also quantified by conditioning on the predicted hydrological conditions in a reference interval that precedes 2012 (see companion submethodology M08 (as listed in Table 1) for receptor impact modelling (Hosack et al., 2018)).
For surface water and groundwater variables in the Hunter subregion, the reference assessment interval is defined as the 30 years preceding 2012 (i.e. 1983 to 2012). For surface water variables in the Hunter subregion, the short-assessment interval is defined as the 30 years preceding the short-assessment year (i.e. 2013 to 2042), and the long-assessment interval is defined as the 30 years that precede the long-assessment year (i.e. 2073 to 2102). For groundwater, maximum drawdown (metres) and time to maximum drawdown are considered across the full 90-year window (i.e. 2013 to 2102) as time to maximum can occur at any time during the modelling period.
In BA, choices about receptor impact variables must balance the project’s time and resource constraints with the objectives of the assessment and the expectations of the community (see companion submethodology M10 (as listed in Table 1) for analysing impacts and risks (Henderson et al., 2018)). Choices should be guided by selection criteria that acknowledge the potential for complex direct and indirect effects within perturbed ecosystems, and the need to keep the expert elicitation of receptor impact models tractable and achievable (see companion submethodology M08 (as listed in Table 1) for receptor impact modelling (Hosack et al., 2018)). Unambiguous responses to hydrological changes and the requirement for expertise to assess these in the BA workshops is critical.
For perennial streams, the qualitative modelling workshop identified five variables (three flow regimes, zero-flow days and groundwater levels) as the key hydrological variables that were thought to: (i) be instrumental in maintaining and shaping the components, functions and processes provided by the landscape class ecosystem; and, (ii) have the potential to change due to coal resource development (Figure 12 and Figure 13). All of the ecological components and processes represented in the qualitative model are potential receptor impact variables and all of these are predicted to vary as the hydrological factors vary either individually or in combination (Table 7 and Table 8). Following advice from participants during (and after) the qualitative modelling workshop, and guided by the availability of experts for the receptor impact modelling workshop, and the receptor impact variable selection criteria (Section 2.7.1.2.3), the receptor impact models were initially conceived to focus on the relationship between flow-dependent macroinvertebrates and riffle-breeding frogs to changes in FR3.
The hydrological factors identified by the participants after the Hunter subregion qualitative modelling workshop have to be interpreted as a set of hydrological response variables. The hydrological response variables are summary statistics that: (i) reflect these hydrological factors; and (ii) can be extracted from BA’s numerical surface water and groundwater models during the reference-, short- and long-assessment intervals defined above. However, due to the reservations surrounding the definition of ‘low flow’, and its sensitivity to the stream channel geometry (which varies across the landscape class), the experts at the receptor impact modelling workshops elected to change the hydrological response variable for the perennial streams from FR3 to zero-flow days (Table 9). The precise definition of the receptor impact variable, typically a species or group of species represented by a qualitative model node, was also determined by the experts during the receptor impact modelling workshop.
Using zero-flow day hydrological response variables, and the receptor impact variable definitions derived during the receptor impact modelling workshop, the relationships identified in the qualitative modelling workshop were formalised into two receptor impact models that predict the response of:
- Mean density of larvae of the Hydropsychidae family (net-spinning caddisflies) in a 1 m2 sample of riffle habitat, to changes in the number of zero-flow days (averaged over 30 years) (ZQD, subsequently referred to in this Section as ‘zero-flow days’) and the maximum length of spells (in days per year) with zero flow averaged over a 30-year period (ZME)
- Mean probability of presence of the riffle-breeding frog (Mixophyes balbus) in a 100-m transect, to changes in ZQD and ZME.
Note that a receptor impact model for investigating the relationship between the annual mean percent projected foliage cover of woody riparian vegetation (Eucalyptus tereticornis, Casuarina cunninghamiana, Eucalyptus camaldulensis; the riparian habitat (RH) node in the perennial streams qualitative model) and FR1, FR2 and groundwater is presented in the ‘Forested wetland’ landscape class analysis (Section 2.7.4.2).
Table 9 Summary of the hydrological response variables used in the receptor impact models, together with the signed digraph variables that they correspond to, for perennial streams in the Hunter subregion
2.7.3.2.3 Receptor impact models
2.7.3.2.3.1 Presence of riffle-breeding frogs
The density and diversity of frogs in streams responds to local, ground-level stream and vegetation variables (Parris and McCarthy, 1999). Many frogs that breed in permanent water bodies are excluded from temporary ones because their larval stage is longer than the persistence of water in these habitats. Therefore, the mix of frog species found in different streams can be partially explained by the different periods of water availability needed by each species in order to breed successfully (Brisbane City Council, 2010).
Elicitation scenarios
Table 10 summarises the elicitation matrix for the presence of the riffle-breeding frog in perennial streams in the landscape class. The first seven design points – design point identifiers 1 to 7 - address the predicted variability in ZQD and ZME across the perennial streams in the landscape class during the reference interval (1983-2012). The design points 1, 2, 4 and 6 capture the combination of the extremes of each hydrological response variable, whilst design points 3, 5 and 7 represent intermediate points in each hydrological response variable axis.
The remaining design points represent hydrological scenarios that span the uncertainty in the values of the hydrological response variables in the relevant time period of hydrological history associated with the short (2042) and long (2102) assessment years. The high and low values for Yref (the value of the receptor impact variable in 2012 on the linear predictor scale) were again calculated during the receptor impact modelling workshop. (Note designs for the reference and future-assessment periods are produced separately and identifiers are not unique across the two.)
Table 10 Elicitation design matrix for the receptor impact model of probability of presence of the riffle-breeding frog (Mixophyes balbus), over a 100-m transect in perennial streams in the Hunter subregion
Design points for Yref in the future (short- and long-assessment periods) are calculated during the receptor impact modelling elicitation workshop using elicited values for the receptor impact variable in the reference period. Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale; it has no value if the design case is in the reference assessment year. All other design points (with identifiers) are either default values or values determined by groundwater and surface water modelling. na = not applicable, ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, ZQD = the number of zero-flow days per year, averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
Receptor impact model
The fitted model for the probability of presence of the riffle-breeding frog takes the form
|
(1) |
where ![]() is an intercept term (a vector of ones),
is an intercept term (a vector of ones), ![]() is a binary indicator variable scored 1 for the case of an assessment in the future period (i.e. short- or long-assessment year),
is a binary indicator variable scored 1 for the case of an assessment in the future period (i.e. short- or long-assessment year), ![]() is a binary indicator variable scored 1 for the case of an assessment in the long-assessment year,
is a binary indicator variable scored 1 for the case of an assessment in the long-assessment year, ![]() is a continuous variable that represents the value of the receptor impact variable on the link transformed scale in the reference year (Yref; set to zero if the design case is in the reference assessment year),
is a continuous variable that represents the value of the receptor impact variable on the link transformed scale in the reference year (Yref; set to zero if the design case is in the reference assessment year), ![]() is the integer value of ZQD and
is the integer value of ZQD and ![]() is the integer value of ZME, all with corresponding fitted
is the integer value of ZME, all with corresponding fitted ![]() coefficients (see Table 3 in companion submethodology M08 (as listed in Table 1) for receptor impact modelling (Hosack et al., 2018)). The (marginal) mean and 80% central credible intervals of the two hydrological response variable coefficients are summarised in the partial regression plots in Figure 14, whilst Table 11 summarises the same information for all seven model coefficients.
coefficients (see Table 3 in companion submethodology M08 (as listed in Table 1) for receptor impact modelling (Hosack et al., 2018)). The (marginal) mean and 80% central credible intervals of the two hydrological response variable coefficients are summarised in the partial regression plots in Figure 14, whilst Table 11 summarises the same information for all seven model coefficients.
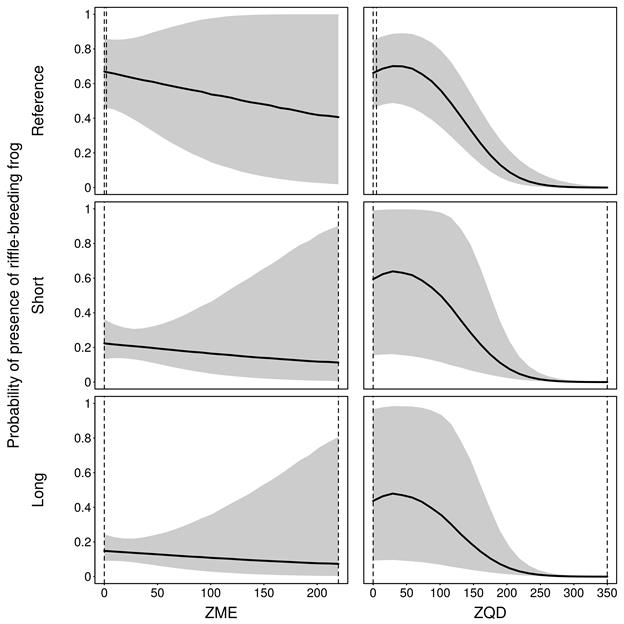
The hydrological response variables in this receptor impact model vary during the reference interval and the future interval. The model indicates that the experts’ elicited information strongly supports the assertion that ZQD has a negative effect on the density of riffle-breeding frogs despite the experts being quite uncertain about its average value. The model suggests that the probability of presence can vary across the landscape class from less than 0.4 to 0.8 under conditions of constant flow (ZQD = 0), holding all other covariates at their mid-values. As the number of zero-flow days increase, however, experts were of the opinion that the probability of presence would drop quite dramatically with the model suggesting some chances of probability of presence near zero under extremely dry conditions (ZQD > 350 days) (Figure 14).
There was very little evidence in the elicited data to suggest that this effect would be substantially different in the future-assessment years. This is indicated by the somewhat identical partial regression plots in the reference, short- and long-assessment years (Figure 14), and the relatively large negative 10th and positive 90th percentiles for the future1 coefficients in Table 11. The model does, however, suggest that the experts’ uncertainty increased for predictions in the long-assessment year (2102) relative to the reference year and that the mean probability of presence in 2102 will be slightly lower (if all other variables remain unchanged).
The elicitation was carried out with the experts deciding to provide responses for scenarios 1 and 7 only. The argument was that under the reference period, the other scenarios were not describing the hydrological conditions of the perennial stream landscape class. Figure 14 reflects this as the dashed vertical lines for the reference period only describe small intervals for both ZME and ZQD.
In middle and bottom rows, all other hydrological response variables are held constant at the midpoint of their elicitation range (during risk estimation all hydrological response variables vary simultaneously). Dashed vertical lines show range of hydrological response variables used in the elicitation. ZQD = zero-flow days (averaged over 30 years), ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
The best-fitting model in this case indicates that the probability of presence of the riffle-breeding frog in the reference years has an influence on its probability of presence in the future years. This is indicated by the fact that ![]() for all presented quantiles in Table 11. This suggestion is consistent with a belief on the part of experts that development would be unlikely to greatly alter the presence of suitable habitat, such that if suitable habitat exists at a location to support a relatively large number of frogs in the reference period then that habitat would be likely to ‘persist’ and continue to support a relatively large number of frogs in the future, despite development.
for all presented quantiles in Table 11. This suggestion is consistent with a belief on the part of experts that development would be unlikely to greatly alter the presence of suitable habitat, such that if suitable habitat exists at a location to support a relatively large number of frogs in the reference period then that habitat would be likely to ‘persist’ and continue to support a relatively large number of frogs in the future, despite development.
Table 11 Mean, 10th and 90th percentile of the coefficients of the receptor impact model for probability of presence of the riffle-breeding frog (Mixophyes balbus) in perennial streams in the Hunter subregion
Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale; it has no value if the design case is in the reference assessment year. Future is a binary variable scored 1 if the analysis case is in a short- or long-assessment year. Long is a binary variable scored 1 if the analysis case is in the long assessment year. ZQD = the number of zero-flow days per year, averaged over a 30-year period, ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, I(ZQD^2) = zero-flow days quadratic term
Data: Bioregional Assessment Programme (Dataset 1)
2.7.3.2.3.2 Density of Hydropsychidae larvae
Hydropsychidae are a family of the order Trichoptera (caddisflies), whose larvae are not usually found in polluted or saline water. Their larval populations can be large in many Australian river systems. The larvae live on rocks, boulders or submerged logs in moderate to fast-flowing waters. Larvae are omnivorous, and a capture net is used to filter food particles from the water column, including algae, organic particles and small invertebrates (Hawking et al., 2009). Along with other benthic invertebrates, they are integral to the movement of energy and matter from the benthos (periphyton) both to higher trophic levels (as a food source for other aquatic biota) and from aquatic systems to terrestrial food webs (as emergent adults) (Runck, 2007). Common genera of caddisflies in south-eastern Australia include Notalina, Hellyethira and Cheumatopsyche.
Elicitation scenarios
Table 12 summarises the elicitation matrix for the density of Hydropsychidae larvae. The first eight design points - design point identifiers 1 to 8 - address the predicted variability in ZQD and ZME across the landscape class in the reference interval, capturing the lowest and highest predicted values together with intermediate values. These design points provide for an estimate of the uncertainty in Hydropsychidae larval density across the landscape class in the reference year 2012 (Yref).
Design points 9 to 23 inclusive (as listed in Table 12) represent scenarios that span the uncertainty in the predicted values of ZQD and ZME in the relevant time period of hydrological history associated with the short (2042) and long (2012) assessment years, combined with high and low values of Yref. The high and low values for Yref were again calculated during the receptor impact modelling workshop.
Table 12 Elicitation design matrix for the receptor impact model of density of Cheumatopsyche spp. (Hydropsychidae) larvae per m2 of riffle habitat in perennial streams in the Hunter subregion
Design points for Yref in the future (short- and long-assessment periods) are calculated during the receptor impact modelling elicitation workshop using elicited values for the receptor impact variable in the reference period. All other design points (with identifiers) are either default values or values determined by groundwater and surface water modelling.
Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale; it has no value if the design case is in the reference assessment year. na = not applicable, ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, ZQD = the number of zero-flow days per year, averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
Receptor impact model
The fitted model for Hydropsychidae larval density takes the form
|
|
(2) |
where the terms ![]() are as before,
are as before, ![]() is the integer value of ZQD,
is the integer value of ZQD, ![]() is the integer value of ZME and
is the integer value of ZME and ![]() Identifies the coefficient for the quadratic term
Identifies the coefficient for the quadratic term ![]() . The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 15, whilst Table 13 summarises the same information for all seven model coefficients.
. The (marginal) mean and 80% central credible interval of the coefficient for this hydrological response variable are summarised in the partial regression plots in Figure 15, whilst Table 13 summarises the same information for all seven model coefficients.
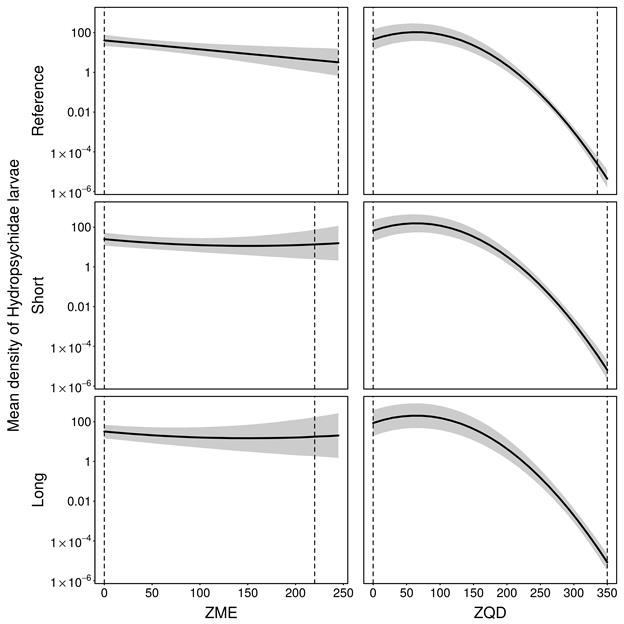
The model indicates that the experts’ elicited information strongly supports the assertion that ZQD has a negative effect on the density of Hydropsychidae larvae despite the experts being uncertain about its average value. The model suggests that mean larvae density can vary across the landscape class from about 50 per m2 to 100 per m2 under conditions of constant flow (ZQD = 0, ZME = 0), holding all other covariates at their mid-values. As the number of zero-flow days increase, however, experts were of the opinion that density would drop dramatically with the model suggesting values less than 1 per m2 as flow conditions become increasingly intermittent (ZQD > 200 days) (Figure 15). Note that in this model the positive effect on mean larval density from the term ![]() is overwhelmed by the negative effect of the
is overwhelmed by the negative effect of the ![]() term. The slight increase in mean larval abundance when zero-flow days increase from 0 to 50 is likely an artefact of the model fitting process rather than an indication of an ecological phenomena. The selection of the quadratic term for both ZQD and ZME is most likely driven by the need to render the sharp decrease in larvae density. This induces a weak artefact signal of increase in larvae density for ZQD values from 0 to 50 days. This artefact signal stems from the need to best fit the elicited data with a shape-constrained curve. The uncertainty around this prediction though mitigates this conclusion and is advocating for a plateau-type signal for ZQD values between 0 and 120 days.
term. The slight increase in mean larval abundance when zero-flow days increase from 0 to 50 is likely an artefact of the model fitting process rather than an indication of an ecological phenomena. The selection of the quadratic term for both ZQD and ZME is most likely driven by the need to render the sharp decrease in larvae density. This induces a weak artefact signal of increase in larvae density for ZQD values from 0 to 50 days. This artefact signal stems from the need to best fit the elicited data with a shape-constrained curve. The uncertainty around this prediction though mitigates this conclusion and is advocating for a plateau-type signal for ZQD values between 0 and 120 days.
There was little evidence in the elicited data to suggest that this effect could be different in the future assessment years. This is indicated by the interaction between ‘future’ and ‘ZME’ which has been selected in the best model (Table 13), and the slightly increasing curvature in the marginal regression plot for ZME in the short- and long-assessment years (Figure 15). In effect the model is saying that the influence of ZME becomes slightly more curvilinear into the future.
Finally, in the canopy cover model for forested wetlands (Section 2.7.4.2) there was strong evidence within the experts’ elicited values that average percent canopy cover in the reference year had a positive influence on the values in the future assessment years![]() ). The model selection procedure in this case, however, has eliminated the possibility that the average density of Hydropsychidae larvae in the reference years has an influence on its abundance in the future years. This is indicated by the fact that
). The model selection procedure in this case, however, has eliminated the possibility that the average density of Hydropsychidae larvae in the reference years has an influence on its abundance in the future years. This is indicated by the fact that ![]() is not included within the best-fitting model (Table 13). This suggestion is consistent with the assertion that (over a 30-year period) there is likely to be very little lag in the response of short-lived species to changes in the hydrological response variables.
is not included within the best-fitting model (Table 13). This suggestion is consistent with the assertion that (over a 30-year period) there is likely to be very little lag in the response of short-lived species to changes in the hydrological response variables.
In middle and bottom rows, all other hydrological response variables are held constant at the midpoint of their elicitation range (during risk estimation all hydrological response variables vary simultaneously). Dashed vertical lines show range of hydrological response variables used in the elicitation. ZQD = the number of zero-flow days per year, averaged over a 30-year period, ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period
Data: Bioregional Assessment Programme (Dataset 1)
Table 13 Mean, 10th and 90th percentile of the coefficients of the receptor impact model for the mean density of Cheumatopsyche spp. (Hydropsychidae) larvae per m2 of riffle habitat in perennial streams in the Hunter subregion
Future is a binary variable scored 1 if the analysis case is in a short- or long-assessment year. Long is a binary variable scored 1 if the analysis case is in the long assessment year. ZQD = the number of zero-flow days per year, averaged over a 30-year period, ZME = the maximum length of spells (in days per year) with zero flow averaged over a 30-year period, I(ZQD^2) = zero-flow days quadratic term, future1:I(ZME^2) = interaction between future 1 and maximum length of zero-flow day spells quadratic term
Data: Bioregional Assessment Programme (Dataset 1)
Product Finalisation date
- 2.7.1 Methods
- 2.7.2 Prioritising landscape classes for receptor impact modelling
- 2.7.3 'Riverine' landscape group
- 2.7.4 'Groundwater-dependent ecosystem' landscape group
- 2.7.5 'Coastal lakes and estuaries' landscape group
- 2.7.6 Limitations and gaps
- Citation
- Acknowledgements
- Contributors to the Technical Programme
- About this technical product