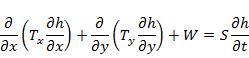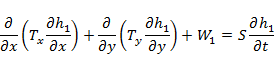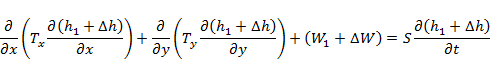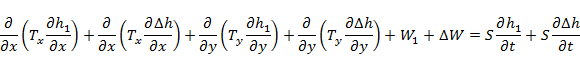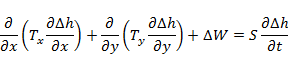2 Modelling philosophy

The objective of groundwater modelling undertaken as part of a bioregional assessment (BA) is to assess the potential impact of coal resource development on water and water-dependent assets.

Generally, the type of modelling undertaken will be trajectory modelling. Two potential futures are considered in a BA:

The difference between CRDP and baseline (known as the additional coal resource development) is the change that is primarily reported in a BA. This manner of using groundwater models is different to the typical use for which many existing groundwater flow models were developed. Therefore, the use of existing models in BAs will need to be evaluated in terms of their suitability for this purpose.

As outlined in the BA methodology (Barrett et al., 2013), one of the overarching goals of the Bioregional Assessment Programme is for results to be transparent and reproducible. Transparency will require that the models and related scripts used in BA analyses are subsequently made publicly available. Reproducibility requires that model runs are undertaken using a documented workflow.

There is an explicit acknowledgement that in all cases not all of the information required to build an ideal groundwater flow model will be available; therefore assumptions will need to be made with regards to model conceptualisation and parameterisation. The uncertainties associated with these assumptions are to be quantified and then propagated from conceptual modelling to receptor impact modelling wherever possible. This will require that models are run probabilistically and not deterministically; consequently, this means that modelling outputs will not be scalar values but probability distributions.

Mismatches in scale between the regional nature of the modelling and the point-scale nature of the model nodes mean that the modelling will not be able to capture fine-scale complexities of impacts upon assets and/or landscape classes. For this reason, results will not be reported in absolute terms but instead as differences between the baseline and CRDP (see Figure 15).

All of the models used in BAs will be ‘Class 1’ models as defined by the Australian groundwater modelling guidelines (Barnett et al., 2012). This is the lowest level of certainty within the classification and is a reflection of the data available and predictions required, rather than the quality of the models. Key indicators of Class 1 models include that model predictive time frames are more than ten times longer than the length of the transient model calibration period, and that the magnitude of stresses featured in prediction scenarios is more than five times larger than simulated in the calibration period (Barnett et al., 2012).

2.1 The principle of superposition

In BA we are interested in the difference between two future model runs, it is the drawdown that we are focused on rather than the absolutes. The principle of superposition is a mathematical concept that applies to linear systems governed by linear differential equations. This is often invoked in groundwater modelling and can be illustrated at its simplest as a doubling of a stress (e.g. pumping) will result in a doubling of the response (drawdown). The principle of superposition is used in BA through reporting of results as the difference between the baseline and CRDP.

The principle of superposition can be demonstrated mathematically for transient groundwater flow in a confined aquifer (Reilly et al., 1987):

Where T is transmissivity in the x and y directions, W is the applied stress (e.g. pumping or recharge) and S is the storage coefficient. For a particular set of stresses (pumping) in space and time W(x,y,t), simplified to W₁, we get a particular groundwater level distribution h(x,y,t), simplified to h₁:

If we now impose an additional stress on the system (additional pumping) , we get a different distribution of groundwater levels, :

As the derivative of a sum is equal to the sum of the individual derivatives, we get:

If the second equation is subtracted from the fourth equation, then we have:

The resulting equation shows that the change in groundwater level distribution (drawdown, ) is only dependent on the change in stress (additional pumping, ). In this way the initial groundwater level distribution (dependent on recharge and boundary conditions) and the initial stresses (e.g. agricultural extraction) become irrelevant to the solution. This principle is used explicitly in the analytical element modelling (Gloucester and Galilee) where the initial groundwater levels are all at 0 and the agricultural pumping and recharge are not simulated.

In cases where non-linear differential equations are used, such as in unconfined aquifers, Reilly et al. (1987) suggest that less than 10% change in saturated thickness probably results in negligible errors if the principle of superposition is used. To minimise these errors we cannot ignore the recharge or agricultural pumping in the models that use unconfined aquifers (such as Namoi and Hunter), however getting the recharge and agricultural extraction absolutely correct is not essential for BA purposes (this limits the applicability of these models for water resource planning).

2.2 The precautionary principle

In the groundwater modelling, the precautionary principle is adopted: impacts are over estimated rather than under estimated. There are many assumptions necessary in building a groundwater model, as long as it can be shown that an assumption over estimates – not under estimates – impacts, the assumption is considered valid for the specific purpose of this modelling. An example is the vertical hydraulic conductivity of aquitards; in the absence of definitive measurements, the full plausible range of this parameter is used in BA modelling.

However, an overly conservative estimate of impact is not desirable either. If there are sound reasons to believe that predicted impacts are deemed unrealistically high (e.g. in comparison to earlier modelling efforts in the bioregion) or in excess of legally defined thresholds (such as the specified drawdown thresholds in the NSW aquifer interference policy), the magnitude of the over-estimation needs to be quantified or assessed more closely.