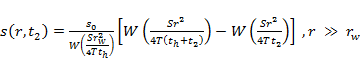The length of model time steps (i.e. stress periods) will be a compromise between (i) the temporal resolution of the outputs required and (ii) achieving feasible model run times while minimising data storage requirements. Laminar groundwater flow is generally a relatively slow process; therefore the use of a daily time step length would be a waste of computational resources. However, in ecological terms, seasonal (i.e. quarterly) variations in baseflow are important; therefore, for BA purposes, this provides an upper limit on the acceptable time step frequency. It has therefore been decided to use a monthly time step length wherever practical for the 90 years of simulation.
It is assumed that after 90 years of simulation the coal seam gas (CSG) and large coal mining development that is simulated has ceased operation. The further into the future we project the impacts of large coal mines and coal seam gas developments the more uncertainty there is in future conditions. These future conditions include the degree to which post-operational conditions have stabilised, the future climate, land use and water sharing rules.
As the modelling is only progressing until 2102 there will be situations where dmax (maximum difference in drawdown for one realisation within an ensemble of groundwater modelling runs, obtained by choosing the maximum of the time series of differences between two futures) has not been reached within this time. After the pumping associated with coal resource development has ceased, dmax at the well will have been reached but the cone of depression can still expand while the pressure is recovering at the well location. This can lead to dmax at a point away from the pumping occurring well after the pumping has ceased. The analytical solution of Yeh and Wang (2009) allows us to investigate the impact of not running the model until dmax is reached:
|
|
(6) |
where s(r,t) is the drawdown at a radial distance from the well r at time t, S is the storativity, T is the transmissivity, rw is the radius of the well and W is the Theis well function. Figure 8 shows a solution of dmax and time to dmax as a function of distance from the extraction well for a case with a T/S of 254 m2/d (this is an example, not related to a specific bioregion). This is showing that close to the well dmax is much greater than when further from the well but time to dmax occurs close to when the pumps are switched off for locations close to the well but time to dmax increases with increasing distance from the pumping well. There is a very clear negative correlation between dmax and time to dmax. For any model node where dmax has not occurred within the temporal domain of the model, dmax must be smaller than every point closer to the pumping well.
Example only; do not use for analysis
dmax refers to maximum difference in drawdown for one realisation within an ensemble of groundwater modelling runs, obtained by choosing the maximum of the time series of differences between two futures
