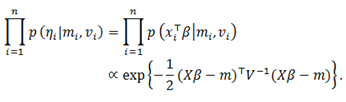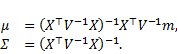- Home
- Assessments
- Bioregional Assessment Program
- Methods
- Receptor impact modelling
- 7 Receptor impact model estimation (stage 6)
This stage constructs the receptor impact models given the specified model structure and the elicited responses contributed by experts, conditional on the hydrological scenarios presented at the receptor impact modelling workshop. The receptor impact models constructed for each landscape class within a bioregion or subregion are reported along with the relevant contextualisation in terms of landscape class definitions and qualitative modelling results in the corresponding product 2.7 (receptor impact modelling) (Figure 3). The method used for the receptor impact model construction is detailed below.
7.1 Prior distribution of beta
Conditional on a design point ![]() , the elicited subjective probability distribution is Gaussian,
, the elicited subjective probability distribution is Gaussian,
|
|
(34) |
The ![]() and
and ![]() are assumed conditionally independent from other elicitations given the design matrix
are assumed conditionally independent from other elicitations given the design matrix ![]() . Let
. Let ![]() and
and ![]() denote a diagonal covariance matrix. The conditional distribution of
denote a diagonal covariance matrix. The conditional distribution of ![]() is proportional to:
is proportional to:
|
|
(35) |
The distribution for the unknown ![]() conditional on
conditional on ![]() ,
, ![]() and
and ![]() is then proportional to a multivariate normal with mean and covariance given by:
is then proportional to a multivariate normal with mean and covariance given by:
|
|
(36) |
7.2 Model structure uncertainty
The full design matrix allows for a quadratic surface response function between the hydrological response function and the receptor impact variables. This includes linear terms, pairwise interactions between the linear terms and quadratic terms for all hydrological response variables. If the hydrological response variables vary in the reference period, then an interaction between the quadratic surface response function and the future period is also included. The full design model structures the elicitation scenario so that this complex model can be elucidated.
However, the full richness of the model may be excessive for simple relationships between hydrological response variables and receptor impact variables. Simpler models are therefore considered. Optional model terms include: interactions between hydrological response variables and the future period, the pairwise interactions between different hydrological response variables and the quadratic terms. The alternative models are ranked using a Bayesian information criterion (BIC) (proportional to the Schwarz criterion; Schwarz, 1978) metric:
|
|
(37) |
where ![]() is the dimension of the vector
is the dimension of the vector ![]() and
and ![]() . The model with the lowest BIC value is selected as the best model.
. The model with the lowest BIC value is selected as the best model.
Note that several terms are required to be retained within all the candidate models. These include: the intercept, the future-period factor, the short-term factor, the influence of ![]() and at least the linear terms of all hydrological response variables to be considered in the receptor impact modelling elicitation workshop. The inclusion of this minimal subset ensures that the covariates which provide the structure for the elicitation scenarios are also represented in the estimation and prediction steps of the receptor impact modelling.
and at least the linear terms of all hydrological response variables to be considered in the receptor impact modelling elicitation workshop. The inclusion of this minimal subset ensures that the covariates which provide the structure for the elicitation scenarios are also represented in the estimation and prediction steps of the receptor impact modelling.

METHODOLOGY FINALISATION DATE
- 1 Background and context
- 2 Identification of potentially impacted landscape classes (stage 1)
- 3 Qualitative mathematical modelling (stage 2)
- 4 Identification of hydrological response variables and receptor impact variables (stage 3)
- 5 Development of scenarios for receptor impact model expert elicitation (stage 4)
- 6 Receptor impact modelling workshop (stage 5)
- 7 Receptor impact model estimation (stage 6)
- 8 Receptor impact model prediction (stage 7)
- 9 Content for product 2.7 (receptor impact modelling)
- References
- Citation
- Acknowledgements
- Contributors to the Technical Programme
- About this submethodology