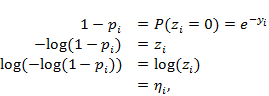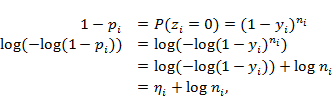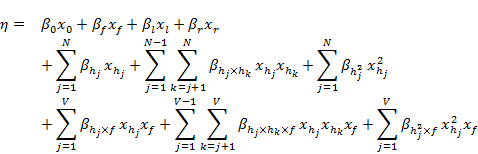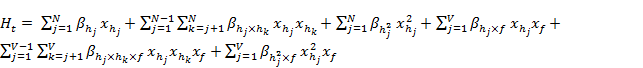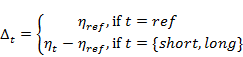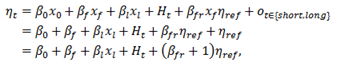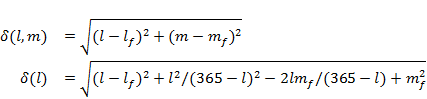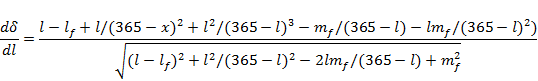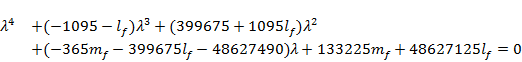As described in Section 1.3, it is essential to have an efficient design to collect expert information given the large number of receptor impact models, landscape classes and bioregions or subregions to address with limited resources. The design must also reflect the predicted hydrological regimes as summarised by hydrological modelling outputs. Without this information, design points may present hydrological scenarios that are unrealistically beyond the bounds suggested by the landscape class definition. Alternatively, insufficiently wide bounds on hydrological regimes lead to an overextrapolation problem when receptor impact model predictions are made conditional on hydrological simulations at the risk estimation stage. The design must further reflect the feasibility of the design space, which may be constrained by mathematical relationships between related hydrological response variables. The design must accommodate the requirement to predict to past and future assessment years. The design must also allow for the estimation of potentially important interactions and non-linear impacts of hydrological response variables on the receptor impact variable. Moreover, the predictions of the receptor impact variable in future years may depend on the state of the receptor impact variable in past years. For example, a forest stand may persist over time periods longer than the time frame considered by BA. The past states of the forest stand may have an important influence on future states; this temporal relationship may also interact with hydrological response variables. Therefore, this ecological temporal relationship, which if ignored may confound the relationship between the receptor impact variable and the hydrological response variables, must also be accommodated for by the design. These above requirements must all be met by the design to enable prediction of receptor impact variable response to hydrological changes at the time points and spatial scales required by BA.
For each landscape class, a set of receptor impact variables (e.g. woody riparian vegetation) and a set of hydrological response variables are defined. For each landscape class, different receptor impact variables may not be connected to the same hydrological response variables. The following section describes the general framework of the elicitation approach.
As noted in Chapter 1, in BAs, hydrological response variables are defined as the hydrological characteristics of the system that: (i) are thought to be instrumental in maintaining and shaping the ecosystem components, processes and functions provided by the ecosystems in each landscape class, and (ii) have the potential to change due to coal resource development. Receptor impact variables are defined as the components of the ecosystem that, according to the qualitative mathematical model developed at the preceding qualitative modelling workshop, potentially change due to changes in the hydrological response variables. Receptor impact models describe how changes in hydrological response variables may impact particular aspects of ecological systems at a project-defined spatial and temporal scale. A receptor impact model describes the distribution of outcomes that would be expected to be observed in a receptor impact variable given a particular change to one or more hydrological response variables.
Where possible, receptor impact models would be based on data. In practice, the empirical information is usually incomplete so structured elicitation with experts is used to integrate their knowledge into the models. The quantitative relationship between receptor impact variables and hydrological response variables is the focus of the receptor impact modelling workshop that follows the qualitative modelling workshop in the overall workflow of the BAs (Figure 3).
The proposed approach allows the elicitation to proceed either on magnitude (e.g. abundance or percent cover) or presence–absence responses. If experts prefer to think about presence–absence for some combinations of covariates, but magnitude for other combinations, then both can be accommodated within a single model. The elicitation target is continuous (i.e. mean abundance or probability). Technical details are given in the following sections.
The structure of the elicitation is as follows. Time is indexed using 
for receptor impact variable responses. Here, refers to a specific year of assessment for the receptor impact variable that corresponds to the pre-specified time points of interest. The complete set of assessment years is given by 
, which corresponds to past, short-term future and long-term future assessment time points, respectively. Associated with each assessment year (that is, for 
) are relevant time periods of hydrological history 
, which vary depending on whether the histories are with respect to groundwater(
) or surface water (
) hydrological response variables. For surface water hydrological response variables, the 
are 30-year time periods with end-date (inclusive). For example, the reference period for all surface water hydrological response variables is given by the closed interval, 
. The groundwater hydrological response variables in the future period are defined relative to the same reference period used for the surface water, 
. The value of the groundwater hydrological response variable depends only on whether or not the assessment year occurs in the reference period or not, and does not depend on whether or not the assessment year occurs in either the short-term or long-term assessment year. For groundwater hydrological response variables, the 
for the short and long periods are therefore the same (
); in this case, the hydrological response variable is, for instance, a summary statistic considered over the whole of the future period. An example is the maximum drawdown in the future period relative to the groundwater level in the reference period. The and , are visualised in Figure 11.
The assessment years, given by 
with 
, were chosen to assess the potential response of the receptor impact variable early in the development period (
), over an intermediate period of development (
) and also the enduring impact of the developments (
). The hydrological response variables (for example, the annual mean number of low-flow days over a 30-year period) were defined by a summary statistic derived for the intervals 
that depended on whether the hydrological response variable was surface water or groundwater (
). The reference period was shared across the hydrology disciplines, 
. The surface water hydrological response variable intervals 
spanned the 30 years preceding . The groundwater hydrological response variable intervals only depended on whether the corresponding assessment year was in the reference or future period; the intervals for the short-term and long-term future assessment years were therefore equivalent for groundwater, 
. The groundwater future interval 
was the only interval that varied depending on bioregion. In this example, 
.
Let 
be a receptor impact variable at time . It is assumed that can depend on:
- hydrological response variables derived for the corresponding intervals
- previous values of the receptor impact variable
.
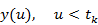The goal of the receptor impact modelling workshop is to predict how the receptor impact variable changes at future time points given the reference value of the receptor impact variable and the hydrological response variable values. The Assessment team therefore elicits subjective probability distributions for the receptor impact variable for particular hydrological scenarios from the experts. The probability distributions express uncertainty in the impact of the hydrological change across the region. For example, the canopy cover of woody riparian vegetation may respond to an increase or decrease of a particular flood expected frequency of occurrence in the 30 years preceding the time point of interest. The predicted receptor impact variable may also depend on the level of the receptor impact variable (e.g. canopy cover) in the past. For example, a change in the hydrological response variable at a future time period relative to the reference period may be relevant if starting from a high level of canopy cover, but perhaps less important if starting from a very low canopy cover. The Assessment team therefore conditions the predictions of receptor impact variables on a stated level of the receptor impact variable at the reference assessment year, which is assumed known. However, the receptor impact variable (e.g. percent cover) at the reference assessment year is actually unknown. Therefore, the experts first assess how the receptor impact variable is distributed across the landscape class at the reference assessment year.
Given the above rationale, the receptor impact modelling workshop elicitation targets are defined by the conditional probability distributions of:
- the receptor impact variable value at the reference assessment year 2012 given any hydrological response variables in the reference period
- the receptor impact variable value at a future year given a value at the reference year and the hydrological response variables during the future time period.
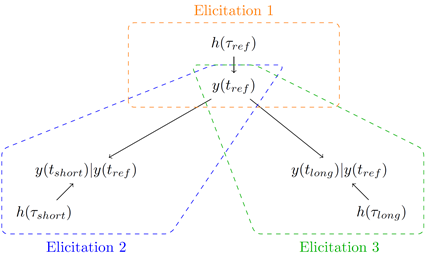
The statistical model and elicitation process is summarised in Figure 12. Note that the final estimated receptor impact variable at time 
depends on the hydrological history prior to 
, but the elicitation has simplified this by conditioning instead on the value of the receptor impact variable at time in the dependence structure of Figure 12. For example, a scenario considered in elicitation 2 (see Figure 12) conditions on the past receptor impact variable (
) instead of the possibly multiple hydrological response variable covariates that correspond to time and period 
.
Figure 12 Elicitation relationship diagram, with the notations used in the related sections
For any 
, the receptor impact variable at time 
depends on the current hydrological response variables (i.e. in the period 
) and the value of the receptor impact variable at time 
.
5.1 The general statistical model
The receptor impact model framework specifies a statistical model for the response function parameterised by expert opinion (Hosack et al., 2016, 2017). A modelling approach is adopted that allows for different types of empirical data, 
, such as abundance, density, quadrat counts or presence–absence using generalised linear models (McCullagh and Nelder, 1989). The observation model for data 
, 
, is assumed to be from the exponential family and is conditioned on the expected response, 
, with possibly additional parameters 
that pertain only to the observation model. This expected response is mapped to the linear predictor, 
, by an invertible link function, 
. The linear predictor depends on the design point defined by the 
vector of known covariate values 
and the vector of unknown coefficients 
through the linear function:
|
|
(16) |
The above assumptions lead to the construction of a prior for the unknown parameters with a generalised linear model with defined observation model, link function and design point .
5.1.1 Choice of link function and observation models
The generalised linear model allows for a wide variety of potentially observable responses that can be identified within a receptor impact model. Many options of link function and observation model will be available for a given receptor impact model. Guidance is provided here to assist this important selection process. The elicitation approach assumes that counts over the non-negative integers follow a Poisson distribution (with unknown varying intensity) and counts from a finite sample size follow a binomial distribution (with unknown varying probability); these are standard choices from the exponential family for count data. For the Poisson case, two link functions will be required (log and complementary log-log, ‘cloglog’), complicating the model fitting. For the binomial case, only the cloglog is required (with and without an offset). For both cases the above approach can be accommodated by the currently available methods for eliciting subjective probability distributions. These choices establish a correspondence among non-negative counts, bounded non-negative counts and presence–absence receptor impact variable models. Although the below choices develop log link models for discrete observations , note that the analogue for non-negative continuous data is given by the Gaussian observation model coupled with log link.
5.1.1.1 Poisson
Let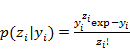 
with 
with mean given by the inverse of the canonical log link function of the linear predictor 
with known covariates and unknown parameters . The intensity of the inhomogeneous Poisson process is given by 
.
5.1.1.1.1 Support
The support of 
is over the non-negative integers, 
. For example, it is applicable to a setting with a countable number of individuals in a given area.
5.1.1.1.2 Elicitation target
The expected value of the response is the average number of individuals in a given area over a specified time period.
5.1.1.1.3 Probability of presence
The probability of observing a zero count is 
. Let 
equal the probability of presence:
|
|
(17) |
where the function 
is called the complementary log log function (cloglog). Therefore, eliciting the probability of presence given the complementary log log link function is a replacement for eliciting the expected abundance, when the expected abundance is very low (near zero). If the expected abundance is far from zero, then the probability of presence is effectively 1 and so will not provide much information on . It is then better to stick to the log link and target the magnitude (e.g. abundance).
5.1.1.2 Binomial
Let 
with mean given by the inverse complementary log log link function 
and linear predictor 
. The expected proportion of presences (successes) is given by .
5.1.1.2.1 Support
The support of is over the bounded non-negative integers, 
. For example, it is applicable to a setting with the number of observed presences given a total number of observations in a given area or transect.
5.1.1.2.2 Elicitation target
The expected value of the response is the expected proportion of presences given the 
observations
5.1.1.2.3 Probability of presence
The probability of observing a zero count is 
. Let equal the probability of presence:
|
|
(18) |
where 
is an offset. The left-hand side on the second line in Equation (18) is again the complementary log log link function, which is also the assumed link function for this binomial generalised linear model. Therefore, the probability of presence given the complementary log log link function is equivalent to eliciting the expected proportion of presences with an offset.
5.1.2 Structure of design matrix
The elicitation of for the short- and long-term future periods depend on the hydrological response variables and a realised value of . The model formulation uses a quadratic surface to describe the relationship between hydrological response variables and receptor impact variables. The curvature allowed for the fact that most ecological variables will have optimal values at intermediate levels of an environmental gradient. For example, not enough water can lead to tree mortality due to drought, whereas too much water can lead to tree mortality due to flooded conditions.
A fundamental issue in developing the receptor impact models is that for a significant number of variables their current state across the landscape class is unknown, which obviously impacts on the ability to make predictions. A key example is groundwater depth. Change in depth can be modelled but there will not be detailed maps of groundwater depth across all subregions or bioregions. Another example is information on the presence, absence or condition of an ecological community. This data will typically be incomplete or missing entirely. Given these constraints, models will sometimes need to accept covariates defined in terms of deviations in hydrological response variables relative to ‘reference’ conditions.
The model structure is determined by the design matrix 
that is composed of the design points 
For hydrological response variables that vary in both the reference and future periods, the functional form is a second order polynomial on the linear predictor that allows interactions among hydrological response variables, the reference period and the future period (Equation 19). For hydrological response variables that are defined relative to the reference period, the values of the hydrological response variables are fixed by definition in the reference period. For a given receptor impact model, enumerate the hydrological response variables with varying values in the reference period by 
, and the hydrological response variables without varying values in the reference period by 
:
|
|
(19) |
The coefficients are defined in Table 3.
Table 3 The coefficient notation, attributed names and corresponding covariates as defined by the structure of the design matrix for the full model
HRV = hydrological response variable, RIV = receptor impact variable
5.1.2.1 Influence of the receptor impact variable from the reference assessment year
Note that by construction the covariate 
named with the symbolic shorthand as 
in Table 3, which has zero values in the reference period, can be interpreted as an interaction between 
and the future period binary factor, 
. To see the ecological interpretation of 
in the above equation for 
that is associated with the covariate (Table 3), which is equivalent to the entrywise product between and 
, first consider a model developed for the unknown quantity 
, with 
a known offset,
|
|
(20) |
where the term:
|
|
(21) |
captures the hydrological response variable effects on the receptor impact variable. The offset is specified as the function:
|
|
(22) |
with the value of in the last line assumed known. Given this specification of the offset, the unknown quantity 
is defined by:
|
|
(23) |
again, with the value of in the last line assumed known.
In the above model for , the term 
measures the association between the receptor impact variable and the future change in 
on the linear predictor scale, and so it includes an interaction with the binary covariate such that this term has no influence on the receptor impact variable in the reference period. The coefficient 
therefore defines the relationship between and the future change when 
The above model for can be rewritten with the known offset moved to the right-hand side:
|
|
(24) |
Consider this model applied to a scenario in the reference period:
|
|
(25) |
where the known offset is set to zero when 
, so that 
. The unknown only appears on the left-hand side, as desired (it is the response variable). For a scenario in the future period with 
, the model instead takes the form:
|
|
(26) |
where 
with known value of for 
. It can be seen that 
for a future scenario. The coefficient associated with the covariate in the original model for above provides the relationship between and the future 
when
All parameters thus have an ecological interpretation. Importantly, dependence of the receptor impact variable on the hydrological response variables is modelled jointly across both reference and future scenarios. Moreover, all unknown parameters appear linearly in the above equations. This linear property will be used by the method of estimation for the unknown parameters described in Chapter 7. For estimation, the choices for the values of in the known offset function are derived from the elicitation scenarios as described in Chapter 7. Future predictions for will depend on known generated in the reference assessment year as described in Chapter 8. Example receptor impact models with specified design matrices are given in Section 5.3.
5.2 Design construction
The selection of design points (or scenarios) for consideration by the experts occurs prior to the receptor impact modelling workshop in two stages. First, potential candidate design points are identified. This stage uses hydrological model output and hydrology expertise to identify plausible bounds on the relevant hydrological response variables. Second, design points are selected from the set of candidate points in such a way to optimise the design subject to the structure of the design matrix as described above.
5.2.1 Candidate point selection
The number of samples 
is set equal to the total number of parameters in the full model that describes the quadratic surface, which fully interacts with the reference period and future period, along with the parameters that correspond to the intercept, the long-term assessment year and the influence of the receptor impact variable from the reference assessment year.
For unconstrained designs, the candidate design points are defined by a 
factorial design with corner points determined by the ranges of the 
hydrological response variables in the reference period. The centre values are typically set to the mid-point of the hydrological response variable ranges for each marginal (Figure 13, top) but occasionally modified, for example, to the logarithmic scale. In the future period, the candidate points are similarly drawn from a 
factorial design for the 
hydrological response variables in the future period augmented by low and high values for the terms: future period, long-term assessment year in the future period and ; this results in a 
factorial design used to generate the candidate set in the future period.
The case of constrained or restricted design regions is considered in Section 5.2.3.
5.2.2 Design point selection
The 
-criterion (Chaloner and Verdinelli, 1995) seeks to maximise the objective function:
|
|
(27) |
where 
, with the notation that 
is a row vector of , and where 
is a probability measure on the design region 
with 
, where is the number of samples at the 
th design point and 
with the total number of samples. The numerical solution uses the optimisation algorithm of Federov (1972) as implemented by Wheeler (2004) and Wheeler (2014) separately applied to the candidate design points generated for the reference and future assessment years. The resulting optimised solutions are randomly ordered within each assessment year. In all cases, the elicitation procedure begins with elicitations in the reference year before progressing to the short-term assessment year and finishing with elicitation in the long-term assessment year (Figure 12).
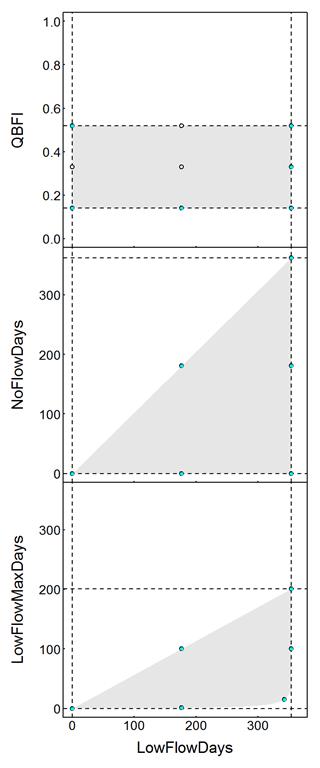
The average number of low-flow days over a 30-year period is given on the x-axis. Top: QBFI, an index of the ratio of surface flow to baseflow, ranges between 0 and 1. The ranges estimated from the stochastic hydrology modelling output are given by black dashed lines. The resulting feasible design region is the shaded area. Candidate design points generated from the 3 by 3 factorial design given by the design region ranges and mid-points are shown by open circles. The cyan points are those selected by the D-criterion optimisation algorithm. Middle: NoFlowDays is similarly defined as LowFlowDays but uses a more extreme flow threshold. NoFlowDays cannot be greater than LowFlowDays, which produces the constrained design region (shaded area). Bottom: LowFlowMaxDays is the maximum duration of low-flow events. The defined relationships between these hydrological response variables result in a complicated set of constraints. The candidate design points affected by the lower bound were adjusted and the revised design points are shown for this example.
5.2.3 Restricted design regions
There are two general strategies to deal with constrained design regions. The first approach would be to propose a set of candidate design points for the unconstrained design region, then optimise the selection of candidate design points from the subset that meet the constraints. The second approach would be to modify the candidate points so as to meet the constraints before optimising the set of design points.
For some elicitations, the first approach is sufficient. For example, in the Gloucester subregion ‘Perennial – gravel/cobble streams’ landscape class percent canopy cover receptor impact model, EventsR0.3 and EventsR3.0, respectively, serve as proxies for overbench and overbank flood events. The number of overbank flood events (EventsR3.0) cannot be greater than the number of overbench flood events (EventsR0.3). Another example is the relationship between the number of no-flow days (equivalently, zero-flow days) and the number of low-flow days. A no-flow day is a day when the flow does not exceed a negligible value, whereas a low-flow day occurs if the daily flow does not exceed a higher value that corresponds to a defined level of low flow. The number of no-flow days therefore cannot exceed the number of low-flow days. This latter example is shown in Figure 13 (middle) for the reference period.
For more restrictive constraint relationships, the simple lattice structure approach to generating candidate points may lose too many candidate points once the constraints are applied. However, in such cases for the receptor impact models considered here, a small adjustment may be applied that brings some of these excluded lattice points back into the feasible design region. The D-optimality algorithm can then be applied to these adjusted candidate points. An example is given below.
This second approach is necessary for combinations of hydrological response variables composed of average number of days of low flow and the average maximum duration of the event, defined as the number of contiguous days separated by a full day over the low-flow threshold. The definitions for these two hydrological response variables impose a complicated set of constraints. The maximum duration of low-flow events within a year, given by 
, must be less than the number of total low-flow days (
), but not below the curve given by 
, thus, 
. Let the coordinates of a non-compliant candidate point drawn from the factorial lattice be given by 
, where 
. The distance from this point to an arbitrary point 
is given by:
|
|
(28) |
where the second line gives the distance to an arbitrary point on the curve that is obtained by substituting 
into the first line. Differentiating this result gives:
|
|
(29) |
Setting 
gives the quartic polynomial equation:
|
|
(30) |
The derivative 
is positive for 
. The curve 
is therefore monotonically increasing within the feasible region and a single real root 
satisfies the constraints, 
. Thus, the solution for the sought-after feasible candidate point is given by the coordinates, 
. A graphical example is given in Figure 13 (bottom). For example, the candidate point in the lower right corner has been visibly adjusted inward to the closest point within the feasible design region.
5.3 Example designs
In this section, two examples are provided from the Gloucester subregion (see companion product 2.7 for the Gloucester subregion (Hosack et al., 2018)). The elicitation scenarios as presented to the experts are provided, and the corresponding design matrices for the full model are presented. The qualitative modelling workshop identified several hydrological response variables to include in the receptor impact modelling for the Gloucester subregion. These are summarised in Table 4. The first example has varying hydrological response variables only in the future period that are defined relative to the reference period. This receptor impact model conditioned on the hydrological response variables: dmaxRef and tmaxRef (groundwater) and EventsR0.3 and EventsR3.0 (surface water). The second example has a single hydrological response variable that varies in both the reference and future periods: ZQD (surface water).
Table 4 Summary of the hydrological response variables used in the receptor impact models for the ‘Perennial – gravel/cobble streams’ landscape class, together with the signed digraph variables that they correspond to for the Gloucester subregion
FR1 = flow regime 1, FR2 = flow regime 2, FR3 = flow regime 3, GW = groundwater
5.3.1 Example with non-varying hydrological response variables in the reference period
One example receptor impact variable in the Gloucester subregion is the mean percent canopy cover of riparian vegetation in the ‘Perennial – gravel/cobble streams’ landscape class. The mean percent canopy cover of riparian vegetation was considered as a temporal average over the assessment year. The area of the hypothetical transect was 2000 m2 covering from the bottom of the stream bench to the high bank. This transect would typically have dimensions 20 m wide by 100 m length but is envisioned to vary with the local stream topography.
This receptor impact model is conditioned on the hydrological response variables (see Table 4): dmaxRef and tmaxRef (groundwater) and EventsR0.3 and EventsR3.0 (surface water). The elicitation scenarios presented to the experts are shown in Table 5. The values of the hydrological response variables are fixed in the reference period by definition. The value of 
, which forms the covariate in Table 3, is not conditioned on elicitations within the reference assessment year of 2012. In the future period, a low and high value for were determined from the 1/4th and 3/4th elicited fractiles (see Section 6.2.2), respectively, from the reference assessment year.
Table 5 Elicitation scenarios considered by the experts for percent canopy cover of riparian vegetation along perennial gravel/cobble streams in the Gloucester subregion
Hydrological response variables are defined in Table 4. Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale.
na = not applicable
The design matrix of the full model with quadratic surface for the hydrological response variable is split into three tables: Table 6, Table 7 and Table 8. The subset of covariates that are retained for all possible models is given in Table 6; compare with the definitions found in Table 3. The new covariate Yrs2tmaxRef, which is assigned zero in the reference period, is simply the difference between tmaxRef and the assessment year, 
. The interaction terms for the hydrological response variables are given in Table 7. Note that there are no interaction terms between the hydrological response variables and the future period binary factor because the hydrological response variables do not vary in the reference period. The quadratic terms for the hydrological response variables are given in Table 8. As described above, the covariates that appear in Table 6 are common to all models. The covariates that appear in Table 7 and Table 8 may potentially be dropped (see Section 7.2), however, forming a candidate set of simpler alternative models relative to the full model.
Table 6 Partial design matrix of the full model for mean percent canopy cover of riparian vegetation along perennial gravel/cobble streams in the Gloucester subregion: essential covariates
Hydrological response variables are defined in Table 4. Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale. Yrs2tmaxRef, which is assigned zero in the reference period, is simply the difference between tmaxRef and the assessment year, 
.
Table 7 Partial design matrix of the full model for mean percent canopy cover of riparian vegetation along perennial gravel/cobble streams in the Gloucester subregion: interaction terms
Hydrological response variables are defined in Table 4. Yrs2tmaxRef, which is assigned zero in the reference period, is simply the difference between tmaxRef and the assessment year.
Table 8 Partial design matrix of the full model for mean percent canopy cover of riparian vegetation along perennial gravel/cobble streams in the Gloucester subregion: quadratic terms
Hydrological response variables are defined in Table 4. Yrs2tmaxRef, which is assigned zero in the reference period, is simply the difference between tmaxRef and the assessment year.
5.3.2 Example with varying hydrological response variables in the reference period
Another example receptor impact variable from the Gloucester subregion is hyporheic (the area beneath the streambed where surface water mixes with groundwater) taxa richness in the ‘Intermittent – gravel/cobble streams’ landscape class. The units are taxa richness per 6 L of water. This receptor impact model is conditioned on the surface water hydrological response variable zero-flow days (averaged over 30 years) (ZQD), which varies in both the reference and future periods. The elicitation scenarios presented to the experts for this example are shown in Table 9.
Table 9 Elicitation scenarios considered by the experts for hyporheic taxa richness within the ‘Intermittent – gravel/cobble streams’ landscape class in the Gloucester subregion
|
Yref |
ZQD |
Year |
|---|---|---|
|
na |
330.3 |
2012 |
|
na |
165 |
2012 |
|
na |
0 |
2012 |
|
6 |
0 |
2042 |
|
12 |
165 |
2042 |
|
6 |
330 |
2042 |
|
12 |
330 |
2102 |
|
6 |
165 |
2102 |
Hydrological response variables are defined in Table 4.
Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale.
na = not applicable, ZQD = zero-flow days (averaged over 30 years)
The design matrix of the full model with quadratic surface for the hydrological response variable is given in Table 10. Note that, in this case, there are no interaction terms between hydrological response variables given the single hydrological response variable. On the other hand, there are interaction terms between the hydrological response variables and the future period binary factor because the values for ZQD vary in both the reference and future periods. The covariates that include interactions or quadratic terms may be dropped, which forms a candidate set of simpler alternative models relative to the full model.
Table 10 Design matrix for the full receptor impact model of hyporheic taxa richness
Hydrological response variables are defined in Table 4. Yref is value of receptor impact variable in the reference assessment year on the linear predictor scale.
ZQD = zero-flow days (averaged over 30 years)
