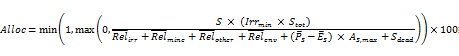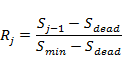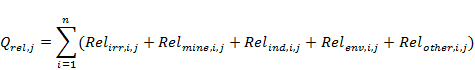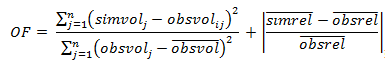Appendix A Modifications to AWRA-R

A.1 Background

AWRA-R was originally developed to provide daily retrospective estimates of water fluxes and stores in both regulated and unregulated river systems. The original model does not include management rules to determine allocations nor control of dam releases. In order to model river flow in regulated reaches, the AWRA-R model needs to determine allocations to compute the dam releases needed as inflow into the river system. To this end, new functionality was developed that performs a resource assessment and simulates downstream water demand (for irrigation, mining, industry, town water) and concurrent releases from major dams.

This new functionality was largely based on existing management rules, which were informed by data and management rules from IQQM (Simons et al., 1996).

Four components were developed to represent the new functionality described above:

These model components are jointly calibrated using both observed data and simulated data from IQQM. They have been developed as a stand-alone model run independently of AWRA-R. Outputs from these components are used as input to the AWRA-R model, which enables it to run more efficiently.

A.2 Modifications

A.2.1 Resource assessment and allocation

A water resource assessment component was developed to estimate the allocation, which is the percentage of the licensed volume for irrigation permitted to be extracted in a water year in the regulated section of the river system. This differs from the IQQM resource assessment which includes all general security licences, whereas all irrigation licences are lumped in AWRA-R. Allocations are computed on 15 August each year and are kept at that level for the remainder of the water year. Again, this differs from IQQM as allocations are computed on 1 July and updated based on resource assessments conducted approximately every fortnight. Allocations cannot go below the level estimated at the previous resource assessment.

To determine the allocation in AWRA-R, the assessment adds the volume of available water in supply dams and subtracts the essential water requirements and losses for the entire river system. The percentage allocation from 15 August onwards is computed as:

where S is the storage on August 14 (m³), Irr_min is a calibrated parameter that represents the minimum proportion of maximum storage capacity below which there are no irrigation allocations, S_tot is the total storage volume for the supply dams (m³), is the mean annual irrigation release (m³), is the mean annual mine release (m³), is the mean annual other release (m³), is the mean annual environmental release (m³) which includes minimum flows and an environmental contingency allowance, is mean annual rainfall on the reservoir (m), is mean annual potential evapotranspiration (m), A_S,max is the maximum storage surface area (m²) and S_dead is the dead storage volume (m³).

A.2.2 Dam storage volumes

The volume of water stored in a dam at a given time-step is a function of the water stored in the dam in the previous time-step, plus the inflows and outflows for the given time-step. Inflows to the storage include rainfall on the reservoir and contributing catchment runoff. Outflows include losses to evaporation, releases from the dam or dam spills. Thus the storage volume of a reservoir on day j can be expressed in the form of a water balance as:

where S_j-1 is storage on the previous day (m³), k is a calibrated scaling parameter, Q_S,j (m/day) is AWRA-L runoff depth, A_cat is the catchment area (m²) contributing to the storage, P_S,j is the rainfall depth on the storage (m/d), E_S,j is potential evaporation depth from the storage (m/d), A_S,j is the surface area (m²) of the reservoir in day j and Q_rel,t is storage release (m³/day).

Leakage from the dam is not explicitly considered in Equation 9 since these data are not available.

Because a dam has a finite storage capacity, there is a volume beyond which the dam will spill because it cannot contain all the inflows. Thus a limit based on dam characteristics is imposed upon the stored volume as:

When S_j>S_full, spillway discharge occurs and is calculated as Q_spill= S_j- S_full. At all other times for S_j≤S_full, Q_spill=0.

During dry periods when the storage is below a calibrated critical threshold (S_min, in m³), but above the dead storage volume, dam releases are reduced in day j by a factor (R_j, which varies between 0 and 1) depending on the storage level and S_min by:

where R_j is the reduction factor (varying between 0 and 1) and S_min>S_dead. Dead storage (S_dead) is water stored in the reservoir below the lowest offtake point, which means that this water cannot be released from the dam.

A.2.3 Dam releases

Dam releases are computed as volumes that satisfy downstream demand for irrigation and industry (including mining, power stations and town water supply). In addition, dam releases are made to meet minimum flow requirements and other environmental flows. Thus, the dam release on day j is the sum of the releases (Rel) to all users along all reaches and is given by:

where for reach i and day j, Rel_irr,i,j is the volume to satisfy irrigation demand, Rel_mine,i,j is the volume to satisfy mining demand, Rel_ind,i,j is the volume to satisfy industry demand, Rel_env,i,j is the environmental release and Rel_other,i,j is other unaccounted releases. All variables are in m³/day.

The daily irrigation release (Rel_irr,i,j) is the amount of water needed to balance a soil moisture deficit, resulting from the difference in precipitation inputs and potential evapotranspiration outputs. Irrigation releases are constrained by: a minimum threshold deficit (Θ_irr,min) below which soil moisture is sufficient to meet crop water requirements and a dam release is not required; allocation (alloc) which limits the amount of water permitted to be extracted for irrigation from the regulated river reaches; maximum irrigable area (A_irrimax) which limits the volume of soil moisture deficit; utilisation in the irrigated reach (I_u), which is the proportion of A_irrimax effectively used; and irrigation system efficiency (I_e), which is the ratio of the volume of water supplied for irrigation to the volume of water consumed by the crop. The daily irrigation release is calculated as:

where Θ_j is the moisture deficit (m) is calculated using a 30-day moving average of daily precipitation P_j (m/day) minus potential evapotranspiration ET_i (m/day) to reflect soil moisture fluctuations, Θ_irr,min ­is the minimum threshold deficit (m), a surrogate of soil wilting point and a calibrated parameter, alloc_j is estimated allocation (dimensionless), A_irrimaxis the maximum irrigable area (m²), I_u ­is utilisation in the irrigated reach and is a calibrated parameter which varies from 0 to 1, and I_e is irrigation system efficiency which is assumed to be 2, which means that half the water extracted from the river is lost through conveyance.

Daily mining releases for each reach are calibrated against modelled monthly mining diversions (DPI Water, Dataset 1) and given by:

where Rel_mine,min is the minimum mine release, Θ_j is the mine water deficit (m) computed similarly as the irrigation moisture deficit, Θ_mine,min is the minimum threshold deficit (m) a calibrated parameter above which mines require water, and A_minemax is the maximum mine ‘area’ in all reaches used as a proxy for water demand, and is calibrated independently using daily mining diversion data for all reaches against simulated mine water demand using a similar approach as for irrigation calibration in AWRA-R (Hughes et al., 2014).

Rel_ind,i,j and Rel_env,i,j are taken directly from the industry and environmental diversions and used as inputs in the calibration. Rel_ind,i,j follows a summer dominated pattern and is estimated manually during calibration.

Rel_other,i,j is an additional release included during testing to improve calibration. It acts as a compensating factor for details not included in the model that were difficult to capture without a more detailed representation. Rel_other,i,j is conceptualised as:

where A_othermax,j is a calibrated parameter.

Table A.1 provides details of the six calibrated parameters in the additional model components for AWRA-R, including units, admissible range and relevance of the parameter.

Table A.1 Optimisable parameters of the four components developed in AWRA-R

Allocation and volumes are calibrated against observed volumes and IQQM releases, in a joint fashion and with the aim of reducing the error and overall bias by optimising the following objective function (OF):

where is the simulated volume time series, obsvol is the observed total dam volume time series, is the mean daily simulated irrigation release time series and is the mean observed daily irrigation release value for the entire system.

The function OF is minimised during optimisation. The optimiser used is the differential evolution algorithm implemented in the R package ‘DEoptim’ (Ardia et al., 2011). This calibration objective function was intended to obtain a parameter set that can simulate dam storage and irrigation release with acceptable accuracy.

The storage volume, releases and allocations are calibrated in the following order:

A.2.4 Rules to simulate industry water discharge

This section refers to a change in AWRA-R that is only applicable to the Hunter subregion.

A simple set of rules to simulate industry water discharge within the Hunter River Salinity Trading Scheme was developed based on the analysis reported in Section 2.1.4.2.4 in companion product 2.1-2.2 (observations analysis, statistical analysis and interpolation) for the Hunter subregion. TableA.2 summarises the streamflow thresholds above which discharges are permitted as a fixed ratio of streamflow, the mean annual discharge volume by Hunter River Salinity Trading Scheme participants during the period 2006 to 2012 and the discharge to streamflow ratio assumed in the AWRA-R model for each reach of the Hunter River Salinity Trading Scheme. Thus when flow reaches 1000 ML/day at stream gauge 210055 on the Hunter River at Denman, the model assumes that the daily discharge from mines in this reach is 0.006*1000 ML/day or 6 ML/day.

Table A.2 Streamflow thresholds and mean industry annual discharge volumes and maximum discharges used in the simplified industry discharge scheme

Data: NSW EPA (Dataset 2)